Технические науки/3. Отраслевое машиностроение

Б.М. Бржозовский, В.В. Мартынов, О.В. Захаров,

Плешакова Е.С., Решетникова Е.П., Автономов М.Э.

Саратовский государственный технический университет имени Гагарина Ю.А., Россия

Исследование эффективности контроля

размеров деталей на токарных станках

В современном автоматизированном многономенклатурном производстве важная роль отводится задаче управления точностью обработки, в том числе с использованием адаптивных методов [1, 2]. Это в свою очередь предъявляет новые требования к эффективности контроля размеров, по которым выполняется коррекция положения инструмента.

Вопрос учета отклонений формы деталей при контроле размеров на токарных станках анализировался в работе [3]. Результаты были получены в предположении, что профиль деталей представляется отдельными гармониками и при расчете справедлив принцип суперпозиций. Однако станок является сложной нелинейной системой, поэтому такой подход можно рассматривать лишь как приближенный. Поэтому предлагается дальнейшее развитие модели контроля размеров и уточнение выводов на основе моделирования для партии деталей.

При контроле на токарных станках наиболее часто используют датчики контакта, фиксирующие отклонение координаты на поверхности детали от некоторого заданного значения. С учетом погрешностей формы и наличия эксцентриситета между осью вращения и геометрической осью детали вследствие различных факторов [2] радиальный размер будет измеряться с методической погрешностью. Очевидно, что эффективность контроля будет зависеть от числа измеряемых точек, методики обработки данных, а также характера отклонений формы поперечного сечения детали.

Известны семь способов измерения [4]: по случайному размеру; по среднему арифметическому из двух взаимно перпендикулярных радиусов; по среднему из трех радиусов, расположенных под углом 120º; по наибольшему радиусу; по наименьшему радиусу; по среднему арифметическому из наибольшего и наименьшего радиусов; по радиусу окружности, полученной методом наименьших квадратов. Перечисленные способы отличаются по трудоемкости (числу измеряемых точек на поверхности), поэтому целесообразно провести их сравнительный анализ и определить область эффективного применения.

Практическое значение имеют следующие методы контроля: по случайному размеру (1 точка); по двум взаимно перпендикулярным радиусам (2 точки); по окружности, построенной по 3 точкам, расположенным через 120º; на основе гармонического анализа с использованием 5 точек (возможно определение 1- и 2-й гармоник профиля).

Расчетная схема контроля представлена на рис. 1. Положение датчика и эксцентриситет между геометрической осью А и осью вращения 0 детали (точнее – проекциями в поперечном сечении) будут переменными величинами как по модулю, так и по угловому положению. Отклонение от круглости d определяется по стандартной методике.

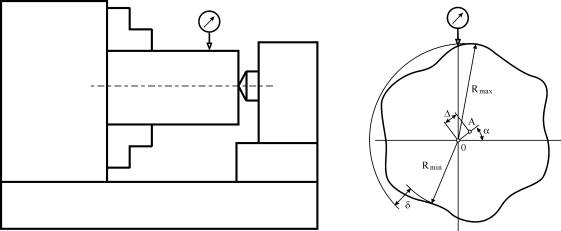
Рис. 1. Схема контроля размера на токарном станке

При измерении по случайному размеру (1 точка) возможно определить только средний радиус R_ср. При измерении двух взаимно перпендикулярных радиусов (2 точки) средний радиус рассчитывался как среднее арифметическое двух измеренных радиусов R_ср = (R_min + R_max)/2, а эксцентриситет в виде их разности D = R_max - R_min. В случае контроля по 3 точкам, расположенным через 120º, находилась окружность, проходящая через эти точки, ее радиус принимался за R_ср, а по координатам центра определялся эксцентриситет. При контроле по 5 точкам с равномерным угловым расположением относительно оси вращения 0 детали расчет проводился в соответствии с гармоническим анализом: нулевая гармоника – средний радиус, амплитуда первой гармоники – эксцентриситет. Данный метод эквивалентен анализу профиля по методу наименьших квадратов. В последнем случае возможно также определение отклонения от круглости в виде разности максимального и минимального радиусов, отсчитываемых от центра А.

В качестве примера рассмотрим контроль размеров при обработке на токарном станке модели МК-3002 по данным работы [5]. Исследовались 5 профилей деталей при 10 случайных реализациях начальной точки контроля. Угловое положение эксцентриситета α также варьировалось по закону равных вероятностей. Результаты моделирования в виде средних арифметических значений оценок искомых параметров представлены в табл. 1. Действительное значение параметров при моделировании является точным.

Таблица 1. Результаты моделирования контроля размеров

Контролируемый параметр	Действительное значение параметра, мм	Измеренное значение параметра в зависимости от числа точек
		1	2	3	5
Радиус Rср Rmin Rmax	10,015 9,985 10,039	10,021	10,013 9,982 10,043	10,018 9,983 10,045	10,014 9,984 10,038
Эксцентриситет D	0,12	̶	0,092	0,104	0,112
Отклонение от круглости d	0,054	̶	̶	̶	0,041

Анализ табл. 1 позволяет сделать следующие выводы:

· при контроле по случайному размеру получается завышенное значение радиального размера, что способствует внесению большей корректирующей поправки и, в конечном счете, приводит к появлению неисправимого брака при обработке;

· при контроле по 2 и 5 точкам получаем несколько заниженное значение радиального размера, что следует расценивать как приемлемый результат;

· наилучшее приближение к действительному значению эксцентриситета обеспечивает контроль по 5 точкам, худшие результаты получаются при 3 и 2 точках, причем характерно занижение значения;

· измерение 5 точек профиля детали позволяет оценить отклонение от круглости, хотя погрешность измерения достаточно велика даже при исключении эксцентриситета на основе гармонического анализа.

Литература

1. Мартынов В. В. Статистические методы обработки экспериментальных данных / В. В. Мартынов, П. В. Мартынов. Саратов: Изд-во Сарат. гос. техн. ун-та, 2011. 188 с.

2. Пуш А. В. Шпиндельные узлы. Проектирование и исследование / А. В. Пуш, И. А. Зверев. М.: Изд-во «Станкин», 2000. 197 с.

3. Правоторова Е. А. Учет отклонений формы деталей при выборе способа измерений в условиях ГПС / Е. А. Правоторова // Измерительная техника. 1987. № 1. С. 15-17.

4. Невельсон М. С. Автоматическое управление точностью обработки на металлорежущих станках / М. С. Невельсон. Л.: Машиностроение, 1982. 184 с.

5. Юркевич В. В. Точность детали в продольном направлении / В. В. Юркевич // Вестник машиностроения. 2001. № 2. С. 34-37.