Технические науки/3. Отраслевое машиностроение

Б.М. Бржозовский, П.Ю. Бочкарев, О.В. Захаров,

Е.П. Решетникова, Е.С. Плешакова, М.Э. Автономов

Саратовский государственный технический университет имени Гагарина Ю.А., Россия

Автоматизированная оценка профиля

продольного сечения цилиндрических деталей

Согласно стандарту [1], прилегающий профиль продольного сечения цилиндрической детали представляет собой две параллельные прямые, соприкасающиеся с реальным профилем и расположенные вне материала. Отклонение профиля продольного сечения есть наибольшее расстояние от точек реальной поверхности до соответствующей стороны прилегающего профиля в пределах нормируемого участка. Частными видами отклонения будут конусообразность, бочкообразность и седлообразность. Количественное нормирование частных видов отклонений не предусмотрено.

Таким образом, задача определения отклонения профиля продольного сечения решается однозначным образом при наличии необходимых средств измерения. В тоже время для оценки формы профиля объективные (количественные) критерии отсутствуют. Это затрудняет автоматизированный анализ результатов измерения. Важное значение данный факт приобретает в зависимости от функционального назначения детали в узле или механизме, когда такие формы отклонений как седлообразность или конусообразность не допустимы по условиям сопряжения. Поэтому в настоящей статье представлена попытка формализовать оценку профиля продольного сечения цилиндрических деталей.

Пусть по результатам измерения получен массив данных (x_i, y_i), где x_i –координата вдоль оси детали, y_i – радиус детали, i = 1, …, n – число измеренных точек. Для дальнейшего анализа необходимо получить аналитический эквивалент профиля. При обработке экспериментальных данных, определённых с погрешностью в каждой точке, имеет смысл взять одну-две базисных функций. Выбор конкретных базисных функций зависит от свойств функции (периодичность, экспоненциальный или логарифмический характер, свойства симметрии, наличие асимптотики и т.д.). В результате получаем систему уравнений вида:

A×U = Y, (1)

где А – прямоугольная матрица размера n×m, сформированная из координат x_i (все строки линейно независимы); U = {u₁, …, u_m}^T – вектор-столбец решения; Y = {y₁, …, y_n}^T – вектор-столбец координат y_i.

В качестве базисной функции целесообразно выбирать гладкие и сравнительно простые функции. Например, в общем случае прямую можно провести через 2 точки, окружность или параболу через 3 точки и т.д. Тогда в системе (1) число уравнений превышает число неизвестных (n > m), ее называют переопределенной и для неё не существует классического решения.

Для решения таких систем используют метод наименьших квадратов (МНК). Его идея состоит в минимизации суммы квадратов невязок:

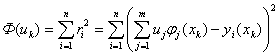, (2)

где k = 1, …, m; j_j(x_k) – базисные функции, например, степенные функции j_j = x ^j.

Решение МНК получается путем приравнивания всех частных производных по компонентам обобщенного решения к нулю (условия минимума):

,

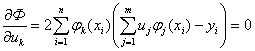и изменяя порядок суммирования, получаем систему линейных алгебраических уравнений вида:

B×U = F, (3)

где B – матрица Грамма; U = {u₁, …, u_m}^T – вектор-столбец решения; Y – вектор-столбец проекций свободного члена исходной задачи на подпространство базисных функций.

Матрица Грамма имеет вид

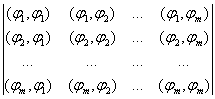, (4)

элементами которой является скалярные произведения .

В правой части системы (3) стоят выражения .

Известно, что матрица (4) симметричная и положительно определенная, таким образом, решение существует и единственно. Находится, например, с помощью итерационного метода Гаусса [2].

Для описания таких свойств профиля продольного сечения, как конусообразность, бочкообразность и седлообразность, предлагается использовать базисные функции в виде степенных. Тогда полином первого порядка дает прямую и позволяет оценить конусообразность, а полином второго порядка – параболу и характеризует бочкообразность или седлообразность.

В результате получаем уравнения прямой y₁ = a₀ + a₁x и параболы y₂ = a₀ + a₁x + a₂x². Значения коэффициентов а в этих уравнения очевидны: a₁ есть тангенс угла наклона прямой к оси детали, a₂ – величина, характеризующая бочкообразность (положительный знак) или седлообразность (отрицательный знак). Составленные матрицы Ф для функций в виде прямой и параболы будут отличаться, поэтому и значений найденных коэффициентов a₀, a₁ также будут различны в этих двух случаях.

Другим важным моментом является анализ погрешностей измерений и полученных на основе их оценок формы профиля детали.

Очевидно, что ошибки в элементах вектора правой части и в матрице системы линейных уравнений (3) могут повлиять на решение этой системы. С практической стороны наиболее актуален случай наличия погрешностей в векторе правой части Y. Здесь можно априори оценить интервал погрешности в зависимости от используемых средств и условий измерений. Тогда мы решаем систему (3) и следующую систему:

B×U₁ = Y + δY, (5)

Предполагается, что каждую из систем мы решаем точно, а основной вопрос – насколько будет отличаться решение U системы (3) от решения U₁ системы (5) с возмущением в правой части δY. Желательно, чтобы при измерении одной и той же величины (радиусов детали) соответствующие решения систем также не очень сильно отличались друг от друга.

В качестве меры близости векторов U и U₁, т.е. вектора ошибки dU = U -U₁, целесообразно взять евклидову норму вектора (предполагая, что имеем нормальный закон распределения параметров):

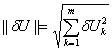, соответственно 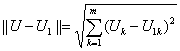(6)

Также для оценки величины матрицы используем спектральную норму в виде квадратному корню из максимального собственного числа матрицы B^-1B:

.

Ошибка в решении системы представляется в виде неравенства:

||δU||/||U|| ≤ cond(B)||δY||/||Y|| (7)

где cond(B) = ||B||×||B^-1|| – число обусловленности матрицы.

Из приведенного неравенства (7) следует, что чем больше число обусловленности матрицы системы, тем больше может быть относительная ошибка.

Таким образом, обоснована методика автоматизированной оценки профиля продольного сечения цилиндрических деталей на основе представления профиля степенными функциями. Это позволяет качественно и количественно оценить частные виды отклонений в виде конусообразности, бочкообразности и седлообразности.

Литература

1. ГОСТ 24642-81. Допуски формы и расположения поверхностей. Основные термины и определения. М.: Изд-во стандартов, 1992.

2. Самарский А.А. Численные методы / А.А. Самарский, А.В. Гулин. М.: Наука, 1989. 430 с.