Построение периодического решения для инерционной передачи

в случае двусторонней силы сопротивления

В работе [1] рассматриваются вопросы построения периодического решения дифференциальных уравнений движения инерционной передачи с рычажным механизмом в случае действия односторонней силы полезного сопротивления. В этой работе проводится построение периодического решения в случае двусторонней силы сопротивления.

Усилим задачу: будем полагать, что угловая скорость ведущего вала . Это предположение затрудняет построение периодического решения, но позволяет судить о неравномерности вращения вала приводного двигателя, повысить соответствие с реальными процессами.

При систему уравнений движения инерционной передачи удобнее записать в координатах [2] с тем, чтобы определять периодический режим по целому числу оборотов грузового звена в относительном движении. Используя соотношение , получим

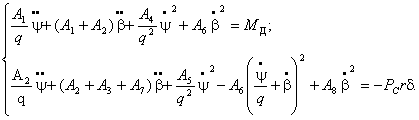(1)

Для определения момента двигателя воспользуемся динамической характеристикой асинхронного электродвигателя.

Решение системы (1), так же как и в случае односторонней силы сопротивления [1], проведем по участкам:

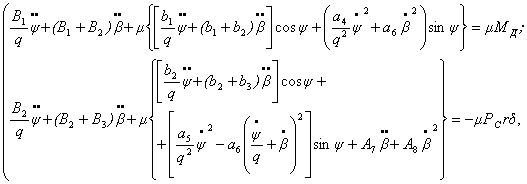Участок 1: . Запишем преобразованные уравнения (1) с введенными при малых членах параметром [2]:

(2)

где

Решение системы (2) будем искать в виде рядов

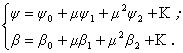(3)

Момент двигателя также представим в виде ряда по параметру

(4)

Подставляя ряды (3) и (4) в уравнения (2) и полагая , получим порождающую систему

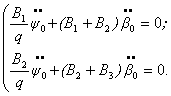
Порождающая система при начальных условиях

имеет следующее решение

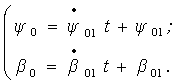
Функции представим в виде рядов

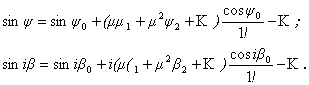
Оставляя в уравнениях (2) лишь члены, содержащие параметр в первой степени, получим систему для определения

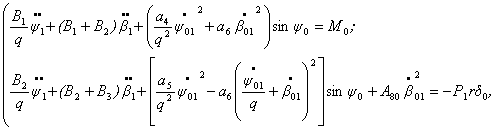(5)

в которой

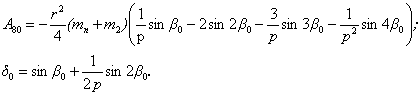
Выражение для найдется из уравнения

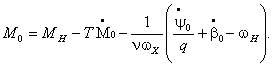(6)

После несложных преобразований уравнение (6) запишем в виде

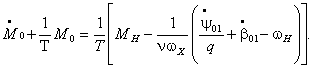(7)

Уравнение (7) является линейным с постоянными коэффициентами. Решая его и учитывая начальные условия , находим

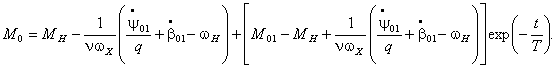(8)

Интегрируя с учетом (8), запишем решение системы (5)

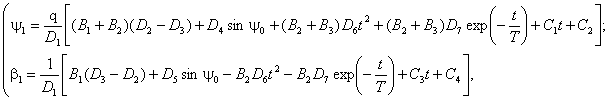
где

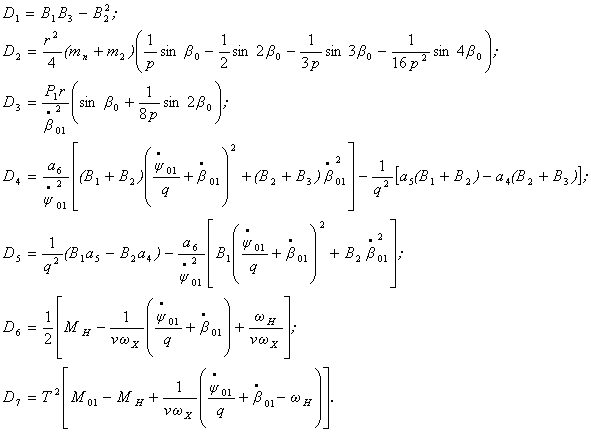
При начальных условиях постоянные интегрирования составляют

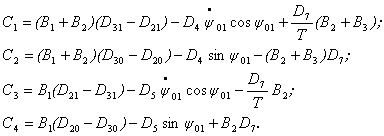
Здесь

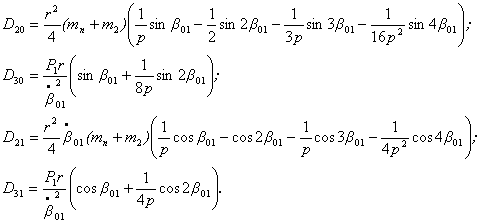
Ограничиваясь в рядах (3) двумя первыми членами, запишем приближенное решение системы (1)

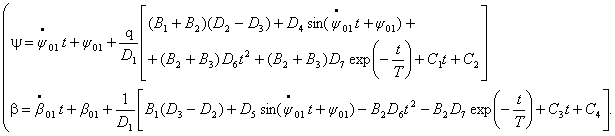
Полученное решение имеет смысл при . При решение порождающей системы примет вид

Тогда система уравнений для и запишется так

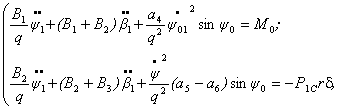(9)

где .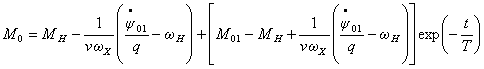

Решая систему уравнений (9), получаем

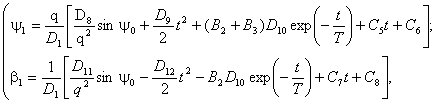
где

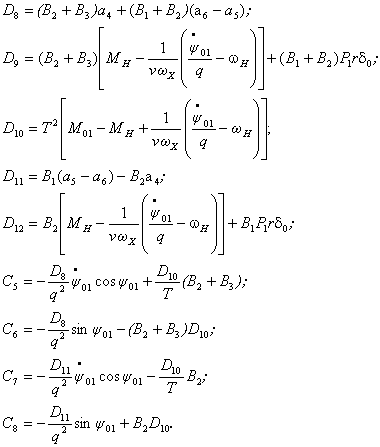
Приближенное решение системы уравнений (1) при этом примет вид

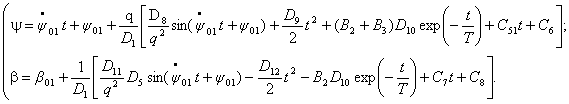
Проверка найденного аналитического решения с помощью численных методов показала высокую сходимость результатов.

Участок 2:  Приближенное решение системы (1) на втором участке получим, положив в решении системы на первом участке вместо значение силы сопротивления .

Участок 3: . Полагаем, что , так как при других значениях и время протекания третьего участка равно нулю.

Подставляя в систему (1), получаем

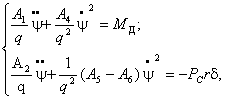
(10)

где

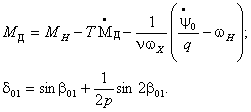
Приближенное решение системы (10) также находим с помощью метода малого параметра

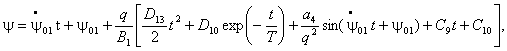
где

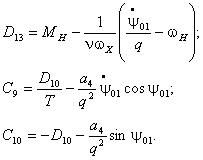
Из второго уравнения системы (10) получаем

.

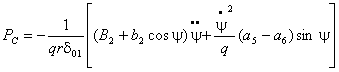Сравнение аналитического и численного решения также показывает высокую сходимость результатов.

Зная решения дифференциальных уравнений (1) по участкам и используя метод припасовывания и метод проецирования траектории изображающей точки, построим периодическое решение уравнений для инерционной передачи с параметрами:

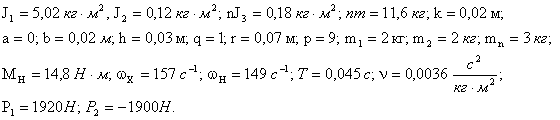
Задавшись произвольными начальными условиями и просчитывая несколько циклов, выходим на замкнутую траекторию, соответствующую устойчивому периодическому решению.

Исследуемая система является фазовой системой, имеющей цилиндрическое фазовое пространство [3,4], поэтому рассматриваем поведение системы по проекциям траектории изображающей точки на цилиндрические поверхности (рис.). Утолщенной линией выделены проекции предельного цикла.

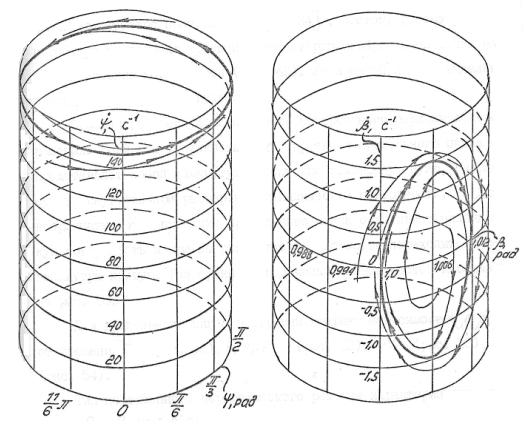
Рис. Проекции траектории изображающей точки

на цилиндрические поверхности

Отметим интересную особенность построенного периодического решения. Если для координаты проекция предельного цикла представляет собой замкнутую траекторию гомотопную нулю, сохраняющую замкнутость при развертке цилиндрической поверхности, то для координаты проекция предельного цикла охватывает цилиндрическую поверхность и при ее развертке на плоскость переходит в незамкнутую кривую. Кроме того, заметим, что, наряду с построенным, возможны и более сложные периодические процессы, которые определяются несколькими оборотами грузовых звеньев в относительном движении.

При построении периодического решения с учетом динамической характеристики двигателя следует дополнительно проверить совпадение значений момента двигателя в начале и конце цикла.

Точка пересечения проекций фазовой траектории в какой-либо одной координатной системе может и не являться особой. Для определения особой точки следует убедиться, что и в другой координатной системе фазовая траектория имеет пересечение с собой в тот же момент времени и дополнительно проверить совпадение значений момента двигателя.

Литература:

1. Алюков С.В. Построение периодического решения для инерционной передачи с рычажным механизмом. Международная научно─практическая конференция «Перспективные вопросы мировой науки», Болгария, 2012.

2. Алюков С.В. Динамика инерционного трансформатора вращающего момента без механизмов свободного хода: Автореф. дис. …канд. техн. наук, ВПИ, 1983.

3. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М.: Наука, 1981, ─ 568 с.

4. Барбашин Е.А., Табуева В.А. Динамические системы с цилиндрическим фазовым пространством. М.: Наука, 1969. ─ 300 с.