Технические науки/8. Обработка материалов в машиностроении

К.т.н. Ботвенко С.И.

Иркутский государственный технический университет, Россия

Распределение закалочных остаточных напряжений

в цилиндре

При изготовлении большинства маложестких деталей из алюминиевых сплавов после механической обработки возникают остаточные деформации в виде различного рода погрешностей. Известно[1, 2], что указанные погрешности в основном это проявление двух факторов - остаточных напряжений имеющихся в заготовке, полученных (наведенных) на стадиях упрочняющей термической обработке (закалке) и остаточных напряжений, вносимых собственно процессом резания. Прогнозирование и расчет остаточных деформаций, в том числе и маложестких деталей, исходя из напряженного состояния заготовки, в настоящее время носит эвристический характер по нескольким причинам. Одной из них является то, что исследователями, занимающихся вопросами изучения остаточных напряжений и деформаций, достаточно хорошо изучены одноосное и плоское остаточно напряженное и деформированное состояние деталей. Использование основных теоретических и эмпирических положений плоского остаточного напряженного состояния применительно к пространственно ориентированным деталям не отвечает предъявляемым требованиям по точности и другим показателям. Таким образом, возникает необходимость в исследованиях пространственного распределения остаточных напряжений в заготовках и деталях.

Рассмотрим цилиндр высотой , который прошел закалку, в результате которой в нем наведены остаточные напряжения. В системе координат, принятой на рис. 1, распределение остаточных напряжений по сечению цилиндра в плоскости ZOY можно описать зависимостью вида

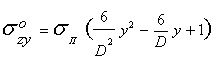, (1)

где: - остаточные напряжения на поверхности цилиндра;

- диаметр цилиндра

Следует отметить, что выражение (1) справедливо для любого осевого сечения цилиндра в плоскости ZOY. Следовательно, объемным представлением распределения остаточных напряжений в цилиндре будет параболоид вращения. Перенесем начало системы координат таким образом, чтобы ось Z совпадала

1

с продольной осью симметрии цилиндра, а оси симметрии его поперечного сечения соответственно совпадали с осями X и Y, при этом направление осей координат остается неизменным (рис. 2). В результате переноса начала координат уравнение (1) для пространственной системы координат примет вид

. (2)

После упрощений

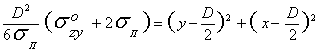. (3)

Введем в выражение (3) значения обобщенных координат, что значительно упрощает дальнейшую работу

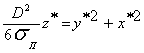. (4)

где:

Для параболоида вращения, изображенного на рис. 2, найдем положение нулевой плоскости, отстоящей на расстоянии от начала системы координат, относительно которой будет выполняться условие статического равновесия. А именно - объем в области сжимающих остаточных напряжений будет равен объему в области растягивающих остаточных напряжений , т.е. в силу начальной симметрии будет выполнено условие

, (5)

Выразим из уравнения (4)

, (6)

2

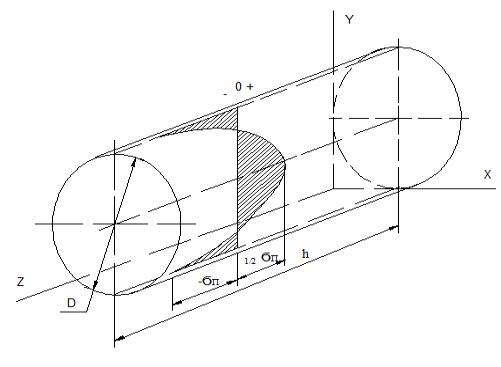
Рис. 1 Эпюра термических остаточных напряжений в цилиндре

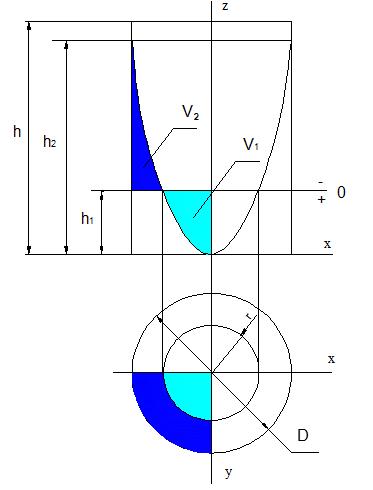
Рис. 2 Распределение термических остаточных напряжений в цилиндре

3

Приравнивая

, (7)

Получим

₍₈₎

При этом величина может быть найдена как

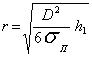(9)

Из равенства

₍₁₀₎

_{Для вычисления объема спроецируем эту область на плоскость XOY. Геометрически этот объем можно описать системой неравенств}

_,

_,

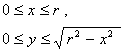_{Согласно [3, 4], объем может быть найден с помощью двойного интеграла}

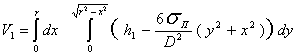_{, (11)}

_{После вычисления внутреннего интеграла получим}

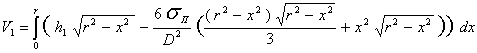_{, (12)}

₄

_{Чтобы избавиться от иррациональности используем тригонометрическую подстановку}

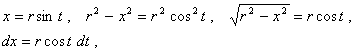₍₁₃₎

_{при .}

_{После подстановки (13) в (14) имеем}

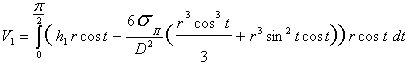_{, (14)}

_{Окончательно}

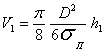_{. (15)}

_{В свою очередь, проекция объема на плоскость XOY представляет собой кольцо, поэтому объем может быть найден как сумма двух объемов с соответствующими проекциями на плоскость XOY}

_{, (16)}

_{Геометрически объем описывается системой неравенств}

_{, (17)}

_{Аналогично для объема имеем}

₍₁₈₎

_{Интеграл для вычисления имеет вид}

₅

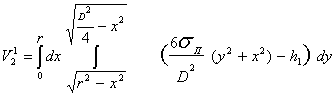_{, (19)}

_{После ряда упрощений окончательно запишем}

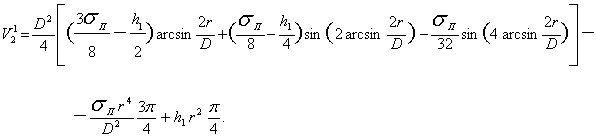₍₂₀₎

_{По (16) определим второе слагаемое}

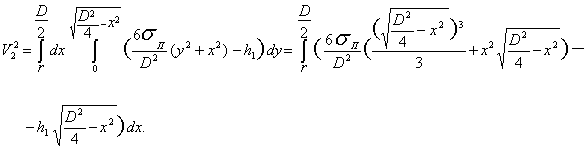(21)

_{Преобразования позволяют получить выражение}

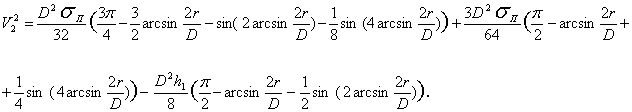(22)

_{Складывая согласно (16), полученные выражения (20) и (22), окончательно имеем}

_{. (23)}

₆

_{Подставим вместо r ее значение, по выражению (1.26), после упрощений окончательно получим}

₍₂₄₎

_{Подставим в условие (1.6) полученные выражения (1.20) и (1.49)}

_.

_{После преобразований получим равенство вида}

_.

_{Таким образом, определено положение нулевой плоскости, относительно которой соблюдается условие статического равновесия объемов в области рас-тягивающих и сжимающих остаточных напряжений в параболоиде вращения (рис. 2) .}

_{Литература:}

1. Zamashchikov Y.I. Machining residual stresses and part distortions. IJMMM,

2007, -Vol.2, No3/4 , p. 378-412

2. Ботвенко С.И. Остаточные напряжения и деформации при изготовлении

деталей типа пластин с подкреплениями. Иркутск: 2012. – 132с.

3. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров

и учащихся вузов. М.: Наука, Гл. ред. физ-мат. лит., 1986. 544с.

4. Кудрявцев Л.Д. Курс математического анализа. В 3т. Т.1, М.: Высш. шк.

1988. 712 с.

7