МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ОЦІНКИ СТУПЕНЯ КРЕДИТНОГО
РИЗИКУ БАНКУ
Мухін
В.
(студент
магістратури ХНЕУ)
Загальна
оцінка ризику, пов’язана з фінансовими можливостями позичальника, може бути
розв’язана методом дискрімінантного аналізу. Останній є розділом факторного
статистичного аналізу, за допомогою якого розв’язуються задачі класифікації,
тобто розбиття деякої сукупності об’єктів, що аналізуються, на класи шляхом
побудови так званої класифікуючої функції у вигляді кореляційної моделі. На
Заході найвідомішими з таких моделей є Z – модель Альтмана і модель
нагляду за кредитами Чессера. Для умов перехідної економіки України необхідно
розробити адекватні моделі, які враховували б галузеві особливості
позичальників і строки кредитування. Частково ця проблема розв’язана.
Розроблені моделі, що дають змогу відокремити позичальників, які мають
прострочену заборгованість за кредитами або за відсотками за ними, від
позичальників, у яких такої заборгованості немає [2]. Розроблені моделі включають такі показники: коефіцієнт
покриття (КП) тобто відношення
поточних активів до поточних зобов’язань; коефіцієнт фінансової залежності (Кфз), тобто відношення позичених
коштів до загальної вартості активів. Наведемо алгоритм знаходження такої
моделі.
Нехай є дві сукупності позичальників: х (без простроченої заборгованості)
та у (з простроченою заборгованістю).
; 
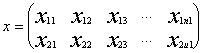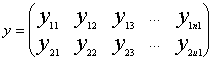; (1)
де n1, n2 – кількість
позичальників сукупності у;
x1j, y1j - коефіцієнти
покриття (Кп);
x2j, y2j
– коефіцієнти
фінансової залежності Кфз , j = 1…,n1; l = 1…, n2.
1. Визначаємо
для матриць вхідних даних х та у оцінки векторів середніх значень 
і 
та коваріаційних
матриць Sх і Sу:
; 
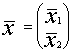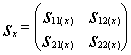; (2)
; 
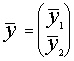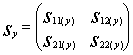; (3)
де 
= 
; 
= 
;
= 
; 
;
= 
; 
;
(j = 1,2; k = 1,2).
2. Розраховуємо
незміщену оцінку сумарної коваріаційної матриці:
[ 
] (4)
3. Обчислюємо
обернену матрицю 
.
4. Обчислюємо
вектор оцінки коефіцієнтів дискримінантної функції:
a = 
( 
) (5)
5.
Знаходимо оцінки дискримінантної функції:
(6)
де 
- транспортовані до х та у матриці.
6. Обчислюємо середні значення:
(7)
7. Знаходимо
межу дискримінації:
(8)
8. Записуємо дискримінантну функцію (модель):
(9)
Якщо Z > C, то
позичальника слід віднести до сукупності х, а якщо Z <С - до сукупності у.
Цей самий алгоритм можна використовувати для розроблення
моделі, яка включає більше двох змінних. При цьому ускладнюються самі
розрахунки.
Проілюструємо
застосування даного алгоритму на прикладі знаходження моделі для позичальників
- підприємств торгівлі з простроченою заборгованістю (табл. 1), та без
простроченої заборгованості (табл. 2).
Таблиця 1
Показники діяльності підприємств торгівлі з
простроченою заборгованістю
|
|
Коефіцієнти |
1. ТОВ «Виал» |
2. ВАТ «Слобода» |
3. ВАТ «Стар» |
4.ТОВ «Еверест» |
5. ПП «Балтика» |
6.ПП «Вітязь» |
7.ПП «МММ» |
8. ТОВ «Мегафон» |
9. ПП «Берізка» |
|
|
|
0,5 |
0,2 |
0,4 |
0,6 |
0,9 |
0,7 |
11,0 |
11,3 |
0,8 |
|
|
|
993 |
666 |
770 |
660 |
887 |
668 |
554 |
668 |
669 |
(%)
1. Визначаємо для матриць вхідних даних х та у оцінки векторів середніх значень х, у та коваріаційних матриць Sx , Sу :
;
Таблиця 2
Показники діяльності підприємств торгівлі
без простроченої заборгованості
|
|
Коефіцієнти |
1.ВАТ «Услада» |
2.ВАТ «Альтек» |
3. ВАТ «Парус» |
4. ПП «Українка» |
5.ТОВ Санхел Україна |
6.ПП «Лаура» |
7.ПП «Аголь» |
8.ТОВ ЗБК-5 |
ТОВ «Сеп-плюс» |
10.ВАТ «Маркет» |
|
|
|
11,0 |
11,1 |
11,3 |
0,9 |
11,1 |
11,5 |
0,8 |
0,5 |
11,3 |
0,8 |
|
|
|
334 |
665 |
773 |
443 |
445 |
550 |
556 |
336 |
447 |
776 |
(%)
Для розв’язання необхідно виконати наступні дії:
величини 
, 
, 
, 
, 
, 
легко обчислити за відповідними формулами.
Обчислюємо також:
;
2. Обчислюємо матрицю 
:
[10 
+ 9 
] =
= 
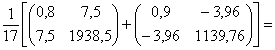
3.Обчислюємо обернену матрицю:
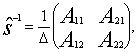(10)
де 
4. Обчислюємо вектор оцінки коефіцієнтів
дискримінантної функції:
5. Знаходимо оцінки дискримінантної функції:
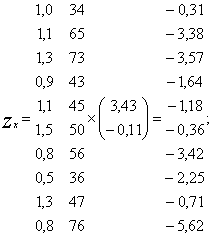
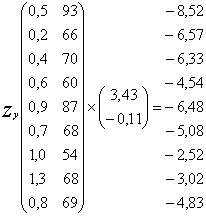
6.
Обчислюємо середні значення:
=
=
7. Знаходимо межу дискримінації:
8. Записуємо дискримінантну функцію (модель):
(11)
Отже модель прогнозування виникнення простроченої
заборгованості позичальників – підприємств торгівлі має вигляд:
(12)
При ZT = 0 маємо
рівняння дискримінантної границі. Для позичальників — підприємств торгівлі, в
яких ZT = 0,
імовірність виникнення простроченої заборгованості за кредитами або за відсотками
за ними дорівнює 0,5. Якщо ZT<0, то ця
ймовірність менша 0,5 і зменшується зі зменшенням ZT, а якщо ZT>0, то вона більша
0,5 і зростає зі зростанням ZT.
Прогнозування виникнення простроченої заборгованості за
кредитами або відсотками за ними за допомогою двофакторної моделі, що включає
коефіцієнти покриття та фінансової залежності, не забезпечує високої точності.
Це пояснюється тим, що дана модель не враховує впливу на фінансовий стан
підприємства інших важливих показників, які характеризують, наприклад, рентабельність,
віддачу активів, ділову активність підприємства. Дискримінантна границя між
позичальниками, що мають прострочену заборгованість, та позичальниками, в яких
вона відсутня, має вигляд не лінії, а розмитої смуги. Помилка прогнозу за допомогою
двофакторної моделі для позичальників — підприємств торгівлі оцінюється
інтервалом, кінці якого можна знайти, підставивши в модель координати точок
і 
, що за моделлю попадають не у свою групу. У результаті
отримаємо інтервал 
Отже, можна зробити таку градацію ймовірності виникнення
простроченої заборгованості залежно від значення Z: до - 1,27 — дуже низька, - 1,27—0 — низька, 0—1,84 —
висока, більше 1,84 — дуже висока. Враховуючи те, що min Кфз = 0, a max Кфз = 100 %, можна зробити такі висновки: для позичальників — підприємств
торгівлі, у яких значення Кфз <
34,4 %, імовірність виникнення простроченої заборгованості за
кредитами або відсотками за ними менше 0,5 незалежно від значення Кп; для позичальників — підприємств торгівлі, в яких значення Кп > 2,1,
імовірність виникнення простроченої заборгованості за кредитами або за
відсотками за ними менше 0,5 незалежно від значення Кфз.
Розглянуті вище розрахунки можна провести за допомогою комп’ютерної
програми STATGRAPHICS. Для
проведення аналізу необхідно занести першочергові дані у таблицю і розділити їх
за окремою класифікаційною ознакою (табл. 3), тобто виокремити позичальників
без проблемної заборгованості (1) від позичальників, які мають проблемну
заборгованість (-1). Коефіцієнти покриття назвемо умовно А1,
коефіцієнти фінансової залежності – А2. В
даному випадку в якості класифікаційної ознаки виступатиме розпізнавання
образів – PR (Pattern Recognition).
На наступному
етапі з’ясовуємо, значення P – Value, щоб дізнатися про
значимість функції. В нашому випадку P – Value дорівнює 0,0085, тобто < 0,05, отже функція значима.
Наступний крок - отримання квадратичного вирішуючого правила. Для цього
необхідні значення показників А1×А2, А1×А1, А2×А2 (табл. 4).
Таблиця 3
Розподіл вихідних даних за класифікаційною
ознакою
|
А 1 |
А 2 |
PR |
А 1 |
А 2 |
PR |
|
1 |
34 |
1 |
0,5 |
93 |
-1 |
|
1,1 |
65 |
1 |
0,2 |
66 |
-1 |
|
1,3 |
73 |
1 |
0,4 |
78 |
-1 |
|
0,9 |
43 |
1 |
0,6 |
68 |
-1 |
|
1,1 |
45 |
1 |
0,9 |
87 |
-1 |
|
1,5 |
58 |
1 |
0,7 |
68 |
-1 |
|
0,8 |
56 |
1 |
1 |
54 |
-1 |
|
0,5 |
36 |
1 |
1,3 |
68 |
-1 |
|
1,3 |
47 |
1 |
0,8 |
69 |
-1 |
|
0,8 |
76 |
1 |
|
|
|
Таблиця
4
Отримані
для розрахунків значення показників
|
А 1 |
А 2 |
PR |
А1×А2 |
А1×А1 |
А2×А2 |
А 1 |
А 2 |
PR |
А1×А2 |
А1×А1 |
А2×А2 |
|
1 |
34 |
1 |
34 |
1 |
1156 |
0,5 |
93 |
-1 |
46,5 |
0,25 |
8649 |
|
1,1 |
65 |
1 |
71,5 |
1,21 |
4225 |
0,2 |
66 |
-1 |
13,2 |
0,84 |
4356 |
|
1,3 |
73 |
1 |
94,9 |
1,69 |
5329 |
0,4 |
78 |
-1 |
28 |
0,16 |
4988 |
|
0,9 |
43 |
1 |
38,7 |
0,81 |
1849 |
0,6 |
68 |
-1 |
36 |
0,36 |
3600 |
|
1,1 |
45 |
1 |
49,5 |
1,21 |
2825 |
0,9 |
87 |
-1 |
78,3 |
0,81 |
7569 |
|
1,5 |
58 |
1 |
75 |
2,25 |
2500 |
0,7 |
68 |
-1 |
47,6 |
0,49 |
4624 |
|
0,8 |
56 |
1 |
44,8 |
0,64 |
3136 |
1 |
54 |
-1 |
54 |
1 |
2916 |
|
0,5 |
36 |
1 |
18 |
0,25 |
1296 |
1,3 |
68 |
-1 |
88,4 |
1,69 |
4624 |
|
1,3 |
47 |
1 |
61,1 |
1,69 |
2289 |
0,8 |
69 |
-1 |
55,2 |
0,64 |
4761 |
|
0,8 |
76 |
1 |
68,8 |
0,64 |
5776 |
|
|
|
|
|
|
Наступним
кроком буде отримання квадратичного вирішуючого правила, представленого в табл.
5.
Проаналізувавши
таблицю, можна сказати, що у 10, 17 та 18 рядках помилкова класифікація. Ця
похибка є допустимою, при такій невеликій групі даних.
Таблиця
5
Квадратичне вирішуюче правило
|
Отримані результати |
Різниця |
PR |
Отримані результати |
Різниця |
PR |
|
1,29995 |
0,299947 |
1 |
-1,05151 |
0,0515125 |
-1 |
|
0,0729404 |
0,92706 |
1 |
-1,06647 |
0,066475 |
-1 |
|
0,240634 |
0,759366 |
1 |
-0,945501 |
-0,054499 |
-1 |
|
0,69493 |
0,305066 |
1 |
-0,372154 |
-0,627846 |
-1 |
|
0,750564 |
0,249436 |
1 |
-0,380107 |
-0,619893 |
-1 |
|
0,90338 |
0,0966197 |
1 |
-0,50148 |
-0,49852 |
-1 |
|
0,003721 |
1,00372 |
1 |
0,276841 |
-1,27684 |
-1 |
|
0,870602 |
0,129398 |
1 |
0,281983 |
-1,28198 |
-1 |
|
0,830993 |
0,169007 |
1 |
-0,393985 |
-0,606015 |
-1 |
|
-0,507884 |
1,50788 |
1 |
|
|
|
Розроблена
математична модель дає змогу відокремити позичальників, які мають прострочену
заборгованість за кредитами або за відсотками за ними, від позичальників, у
яких такої заборгованості немає. Така модель допоможе банкові уникати
кредитного ризику, а отже й нарощувати прибуток.
Література
1. Ефімова Л.Г.
Банківське право: підручник / Л. Г. Ефімова. – К.: Видавництво БЕК, 2006. – 340 c.
2. Жуков Е. Ф. Банки и банковськие операции / Е. Ф. Жуков. – М.: ЮНИТИ, 2005. – 524 c.
3. Жуков Е. Ф. Менеджмент и маркетинг банка: учебное пособие / Е. Ф. Жуков – М.: Банки и биржи, ЮНИТИ,
2007. – 191 с.