Современные информационные технологии /1. Компьютерная инженерия

К.т.н. Аждер Т.Б.

Московский государственный университет приборостроения и информатики

АЛГОРИТМ ИНТЕЛЛЕКТУАЛЬНОЙ ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЙ В ЗАДАЧАХ ОПТИМИЗАЦИИ

В настоящее время информационные технологии используются практически во всех областях человеческой деятельности. С их помощью строятся модели предметных областей для решения задач, таких как управление, поддержка принятия решений и т.д. Выделяют класс трудно формализуемых предметных областей, которые используются, в частности, для решения задач при наличии неполной информации. К данному классу можно отнести задачу диагностики технических систем, т.к. сам факт поиска дефекта объекта говорит об отсутствии полной информации о рассматриваемом объекте. Процесс определения дефекта является задачей поиска оптимального решения из ряда возможных.

При разработке алгоритма интеллектуальной поддержки принятия решений в задачах оптимизации предлагается использовать 2-слойную нейронную архитектуру (рис. 1), т.к. нейронные сети, позволяют решать любые по сложности задачи. Первый слой состоит только из гипотез h₁, h₂, …, h_n (предположений о причине появления дефекта), а второй – из элементов данных d₁, d₂, …, d_m (состояние объекта в рассматриваемый момент времени).

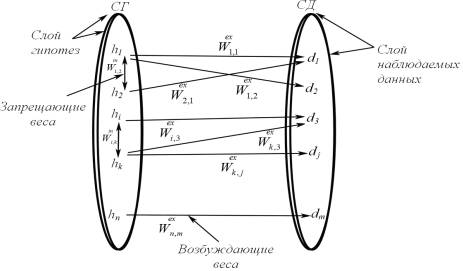
Рисунок 1. Структура двухслойной сети

Эти два слоя связаны весами:

– возбуждающий вес (между гипотезами и данными);

– запрещающий вес (между двумя гипотезами, служит для выявления противоречащих друг другу гипотез).

Алгоритм работы данной модели основан на принципе конкуренции гипотез.

Алгоритм конкуренции гипотез

1. Задаются значения для каждого элемента наблюдаемых данных x_j.

2. Задаются значения возбуждающих весовых коэффициентов – степень доверия, с которой i-ая гипотеза объясняет j-ый элемент данных.

3. Вычисляются значения каждой гипотезы по формуле:

,

где ,

A = 1,

i – принимает значение от 0 до n, n – количество гипотез,

j – принимает значение от 0 до m, m – количество элементов данных.

4. Изначально запрещающим весам присваиваются значения, равные нулю:

.

5. Обновляются значения возбуждающих весов.

,

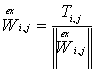где 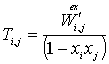, , 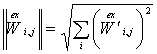– значения возбуждающих весов на предыдущей итерации.

6. Если , то . Происходит сокращение количества конкурирующих гипотез.

7. Вычисляются обновленные значения

.

8. Гипотезы исследуются на возникновение противоречий.

, , ,

где – обновление значений,

– значение на предыдущей итерации,

– разница значений x_i и x_k на двух итерациях.

9. Вычисляются новые значения гипотез:

.

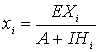10. Если значения гипотез стабилизировались, то решением становится гипотеза с наибольшим значением x_i. Иначе повторяются шаги 5-10.

Данную модель можно использовать только для решения простых задач, когда одна гипотеза независимо от других может полностью объяснить данные. Для решения более сложных задач необходимо реализовывать алгоритм конкуренции гипотез на трехслойной архитектуре сети.

Литература:

1. Бурлаченко Т.Б. Нейросетевая оптимизация абдуктивных выводов в задачах диагностики технических систем / Бурлаченко Т.Б., Морозова Т.Ю. // Мехатроника, Автоматизация, Управление. М., 2008. № 8

2. Люгер Дж. Ф. Искусственный интеллект: стратегии и методы решения сложных проблем, 4-е изд. Пер. с англ. М.: Издательский дом “Вильямс”, 2005.

3. Финн В.К. Интеллектуальные системы и общество / Финн В.К. М.: РГГУ, 2001.