Наметбаев Г.Ш., Чернявская
Н.П.,Туленбаев Ж.С.
Таразский государственный университет им.М.Х.Дулати, Казахстан
МЕТОДИКА ОБРАБОТКИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
ДЛЯ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ.
Наиболее
распространенной методикой построения математических моделей по результатам
измерений входных и выходных сигналов является метод регрессионного анализа.
Однако при отсутствии априорной информации об исследуемом сложном объекте и наличии существенных погрешностей
при отдельных измерениях сигналов во
время проведения пассивного эксперимента решение не всегда достигается. В
подобных случаях большое распространение получил для построения математической модели в место традиционного регрессионного анализа Метод группового учета
аргументов, МГУА (Group Method of Data
Handling, GMDH)
Рассмотрим основные
положения многорядного алгоритма МГУА. Пусть задана совокупность экспериментальных
значений входных переменных:
(1)
и выходной величины Y, где Хi,
i=1,2,…, М, а также У суть N-мерные векторы, N - число точек
в таблице исходных данных, М - число переменных. Формальные
математические модели объектов, описывающие статические режимы их
функционирования, ищутся чаще всего в виде уравнений:
(2)
где А - вектор
неизвестных коэффициентов размерности к; 
Если порядок полинома по всем переменным Xi равен числу M входных координат, то
получаем выражение, которое является полным полиномом Колмогорова-Габбора.
Формализованное
определение алгоритма МГУА, охватывающий максимально широкий класс имеющихся, а
также гипотетических алгоритмов МГУА, дается в [1]. Рассмотрим матрицу Gr,
которую назовем матрицей частных описаний r-го ряда
(3)
Соответствующую задаче
восстановления зависимости по таблице входных переменных:
(4)
и выходной величине
У. Здесь Zi, i= 1,2,...,Q; N - мерный вектор.
Дать определение
многорядного алгоритма МГУА это значит: а) определить G0; б) определить
оператор R, осуществляющий отображение 
; в) определить правило останова; г) определить
значение fr , свободу выбора на r-ом шаге селекции, которая в
общем случае может быть величиной переменной от ряда к ряду.
В качестве G0 выбирается матрица
вида:
, (5)
где δ – либо
нулевой, либо единичный N-мерный вектор.
Частным описанием r-го
ряда, в общем случае, назовем N-мерный вектор Z, если он равен: а) либо
0; б) либо 1; в)
либо k-я компонента его выражается формулой:
, (6)
Наиболее
распространенными частными описаниями являются функции следующего вида:
1)
линейные частные
описания
(7)
2)
квадратичные частные
описания
(8)
3)
частные описания,
содержащие ковариацию
(9)
где индексы i и j изменяются в следующих
пределах: i=1,2,..., Q-1; j= i+1, i+2,…,Q. Введем понятие структуры
частного описания S, как совокупность индексов, соответствующих данному
частному описанию, если оно построено по формуле (9).
Пусть критерием селекции
выбран критерии СR, которому согласно работе [2] соответствует
некоторая матрица D канонической формы, т.е. симметрическая положительно
полуопределенная матрица, позволяющая записать
величину критерия в виде:
(10)
Пусть теперь Σr
- множество всех допускаемых частных описаний r-го ряда. Пронумеруем эти структуры
так, чтобы выполнялись неравенства:
(11)
Можно определить оператор
R как оператор, осуществляющий следующее отображение: матрице Gr-1
ставится в соответствие матрица Gr, столбцами которой с
первого по f-ой являются частные описания, соответствующие структурам 
, 
,..., 
, а столбцы с (F+1)-го по Q-й совпадают с матрицей 
.
Останов многорядного
алгоритма МГУА осуществляется при выполнении условия:
(12)
Для реализации алгоритма
МГУА необходимо, исходя из особенностей поставленной задачи идентификации моделируемых
процессов, определить параметры алгоритма МГУА:
- тип частного описания;
- вид критерия селекции;
- способ разбиения множества точек.
С целью определения
параметров алгоритма МГУА был проведен литературный обзор и поставлен ряд
численных экспериментов на ЭВМ.
Многорядные алгоритмы
МГУА, применяемые для структурной и параметрической идентификации, используют
три вида частных описаний.
Создаваемая математическая
модель всего производства, являющегося сложной системой, используется в данной
работе для оперативной оптимизации. В этом случае значительную роль при выборе
вида частного описания играет наряду с точностью описания простота структуры
конечных уравнений математической модели. Очевидно, что наиболее удобным
является линейная форма математической модели. Поэтому исследовались
возможности построения математических моделей линейной формы и в виде полиномов
второй степени.
Авторами
метода рассмотрено большое число различных критериев выбора моделей.
Значительная часть этих критериев опубликована на сайте http://www.gmdh.net.
Отмечается, что в задачах идентификации необходимо использовать тот или иной
вид критерия минимума смещения.
В работе [2] рассматривается
метод оптимального разбиения исходных данных на основании анализа функций
распределения критерия селекции. Реализация предложенного алгоритма оптимизации
разбиения сталкивается с трудностями,
связанными с большим перебором возможных разбиений. Соотношение размеров
последовательностей может определяться по методу, изложенному в [2].
Рекомендуется выбирать
следующие разделения опытных данных:
для критерия минимума смещения
NA=0,5N; NB=0,5N; NC=0; ND=0. (13)
NA=0,4N; NB=0,4N; NC=0,1N; ND=0,1
где NA, NB, NC, ND
- число точек обучающей проверочной, первой и второй экзаменационных
последовательностей соответственно.
Строгого доказательства
преимущества того или иного метода не существует. Следовательно, проведение
численных экспериментов, для каждого конкретного класса задач, решаемых МГУА,
является наиболее общим и наиболее убедительным методом решения данного
вопроса. Для определения этих параметров были проведены численные эксперименты
с использованием программы SELEC
0.2 являющейся обновленной версией ранее опубликованной программы SELEC 0.1.
Основное меню довольно просто и методика применения его очевиден из самого
интерфейса (рисунки 1 и 2).
Рисунок 1 – Интерфейс программы SELEC0.1
Рисунок 2 – Ввод исходных данных программы SELEC 0.1
Как уже
отмечалось, для описания подсистем практически любых систем химической
технологии и, в том числе производства строительных материалов достаточна форма
полинома второй степени.
Для
построения математических моделей в виде полиномов второй степени был выбран
линейный вид частного описания с расширенным исходным базисом переменных, за
счет переобозначения членов второй степени. Если вектор входных переменных 
, то селекции, в этом
случае, участвует расширенный базис, формируемый по
выражению
(14)
Размерность
входного вектора возрастает
(14)
где 
.
Для
определения наиболее эффективного режима работы алгоритма SELEC0.1 в данной
модификации был поставлен ряд численных экспериментов, результаты
которых приведены на рисунке 3. В качестве объекта моделирования взята СХТС производства изопропилбензола. Из рисунке 3а видно, что характер влияния cпособa разбиения
на глубину минимума критерия в области 
носит
случайный характер. Значительное уменьшение этого соотношения приводит к менее
эффективным решениям. Увеличение свободы выбора F , как видно изрисунка
3б не приводит к ощутимым изменениям глубины минимума критерия селекции. В
связи с этим необходимо определять свободу выбора исходя из времени счета.
Малое значение F приводит к значительному увеличение числа рядов
селекции (рисунок 3в), что в свою очередь приводит к увеличению времени счета.
Значительное повышение значения F уменьшает число шагов селекции, но
увеличивает время счета при переборе пар на каждом шагу селекции. Наиболее
оптимальным является значение F = 10-20. На рисунке 3г представлен
график изменения минимума критерия селекции при выбранных наиболее эффективных
параметрах режима работы алгоритма:
F=15.
Используя
полученные параметры, построены математические модели технологической линии.
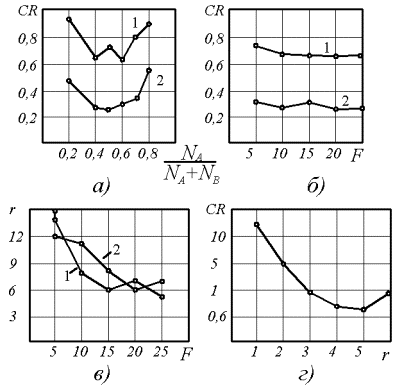
1 – для
кирпича; 2 – для плитки.
Рисунок 3 –
Влияние режимных параметров алгоритма
Литература
1.
www.gmdh.net
2. Mueler J.A., Lemke
F. Sel–organising Data Mining: An Intelligent Approach To Extract Knowledge From Data. – Berlin:
Dresden, 1999. – 225 p