Математика/5. Математическое моделирование

Baimankulov A.

Kostanay State University named after A.Baitursynov, Kazakhstan.

Limitation of coefficient of diffusion

Earlier we received a recurrence relation of calculation of coefficient of diffusion

. (1)

We will prove limitation using aprioristic estimates of the solution of a straight line and interfaced tasks.

From equality , after summation on the ratio follows .

From here

. (2)

Sum up on from the any to and taking into account boundary conditions we have equality

.

We estimate from above this size, that is

.

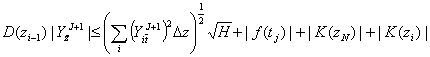If , that on the basis of earlier received estimates

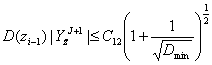. (3)

Using the similar scheme for the interfaced task, we’ll get

.

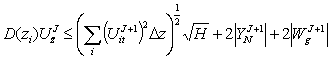Sum up on , then taking into account aprioristic estimates we have an inequality

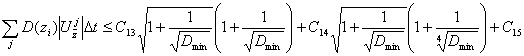(4)

From (2) on a basis (3) и (4), after some transformations the inequality is removed

.

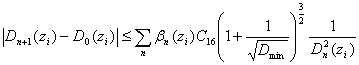Function is selected so

, .

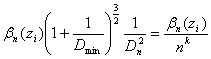In this case we receive that .

Function is selected so that the inequality took place

.

Then performance of the following inequality doesn't raise doubts , .

References

1.Нерпин С.В., Юзефович Г.И. О расчете нестационарного движения влаги в почве// Доклады ВАСХНИЛ, № 6, 1966.

2.Юзефович Г.И., Янгарбер В.А. Исследование нелинейного уравнения влагопереноса. // Л.: Колос. Сб. трудов по агрофизике, вып. № 14, 1967.

3.Байманкулов, А.Т. Конечно-разностная аппроксимация прямой и сопряженной задач [Текст] / Байманкулов А.Т., Махамбетова Г.И. // Materialy IX miedzynarodowej naukowi-praktycznej konferencji «Europejska nauka XXI powieka-2013» Volume 27. Matematyka. Fizyka. Budownictwo i architektura.: Przemysl. Nauka i studia - C.22-23.