Е. Н. Надымов

АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПРИСОЕДИНЕННЫХ МАСС

КАПЛЕВИДНЫХ ОСЕСИММЕТРИЧНЫХ ТЕЛ

На сегодняшний день точные формулы для расчета присоединенных масс (ПМ) в пространственном случае известны только для эллипсоидов. Для остальных объектов используют различные приближенные приемы, при этом исходное тело заменяется другим, сходным с ним по форме [1]. Таким образом, расширение класса тел, для которых известны аналитическое представление ПМ является на сегодняшний день актуальной проблемой. В данной статье рассматриваются каплевидные осесимметричные тела и находятся точные значения ПМ длR екания. В дальнейшем эти тела могут быть использованы для расчетов ПМ объектов с более сложной геометрией.

Каплевидные осесимметричные тела введены впервые при решении задач теории локального взаимодействия [2]. Если за ось вращения принять , то образующие таких тел в параметрической форме представляются следующим образом

где в качестве параметра берется естественный параметр , а – угол между осью тела и касательной к образующей, . Например, уравнения образующих тел, допускающих решения простейшего варианта третьей обратной задачитеории локального взаимодействия, могут быть записаны в виде [2]

где – полином степени , – максимальное значение в носке тела.

Мы ограничиваемся наиболее простыми тела с данными образующими при , так что

	(1)
	(2)

Графики образующих (1) и (2) для приведены на рис. 1 и 2.

Кинетическая энергия жидкости вне поверхности движущегося тела представляется следующей формулой [3]:

где – плотность жидкости, – потенциал скорости набегающего потока, – производная по нормали. Для расчета внешнего осесимметричного обтекания каплевидного тела возьмем в меридианных плоскостях эллиптическую систему координат , связанную с соотношениями

где величина представляет собой расстояние фокусов семейств координатных линий (софокусных эллипсов и гипербол) от начала координат.

Положим

1. Кинетическая энергия продольного (вдоль оси ) обтекания

Так как потенциал в данном случае не зависит от угловой координаты , для элемента поверхности может быть получено следующее выражение:

где обозначает элемент длины меридианного профиля. Отсюда,

Если тело движется в направлении его оси симметрии с постоянной скоростью , то краевые условия представимы в виде

или в эллиптических координатах

Таким образом, получаем выражением для кинетической энергии

Подставляя потенциал продольного обтекания, находим общее представление для кинетической энергии [4]

(3)

2. Кинетическая энергия поперечного обтекания

В случае поперечного обтекания потенциал скорости зависит не только от эллиптических координат и , но также и от цилиндрической координаты . Таким образом, выражение для элемента поверхности будет иметь вид

а уравнение для кинетической энергии, соответственно,

Если тело движется в направлении оси с постоянной скоростью , то граничные условия выражаются уравнением

Потенциал поперечного обтекания можно записать следующим образом [4]

(4)

Как и в случае продольного обтекания, первый множитель подынтегральной функции разложим по полиномам Лежандра

где коэффициенты находятся по формулам:

Следовательно, исходная подынтегральная функция выражается в виде суммы произведений полиномов Лежандра

Аналогично продольному обтеканию, подставляя решение для каждого из интегралов

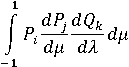
в уравнение (4), можно получить общее аналитическое представление для кинетической энергии продольного обтекания каплевидного осесимметричного тела.

Рассмотрим первый интеграл

Он представим в виде , а при вычисляются следующим образом

где , а – -ый столбец матрицы

Аналогично могут быть получены и остальные коэффициенты . Вычислив , запишем окончательное значение кинетической энергии поперечного обтекания

Из известной кинетической энергии и объема каплевидного тела коэффициент ПМ находится по формуле

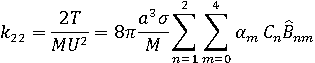
3. Смешанные присоединенные массы

Зная потенциал продольного и поперечного обтекания, можно найти смешанные присоединенные массы и :

Для присоединенной массы с учетом формул (3) и (4) будем иметь:

(5)

Как и в случае продольного обтекания разложим первый сомножитель по полиномам Лежадра . Имеем

где , а коэффициенты имеют представление:

Таким образом, исходная подынтегральная функция представляется в виде суммы произведений полиномов Лежандра

Аналогично выкладкам для случая поперечного обтекания находим каждый из интегралов

и подставляем в уравнение (5). Далее получаем общее аналитическое представление для смешанных присоединенных масс каплевидного осесимметричного тела:

или переходя к коэффициентам и

Таким образом, получены аналитические формулы для вычисления ПМ каплевидных осесимметричных тел, у которых зависит линейно от . При увеличении числа коэффициентов в разложении по степеням выражения для коэффициентов ПМ могутбыть получены аналогичным способом.

Рис 1. Образующие каплевидных тел ()

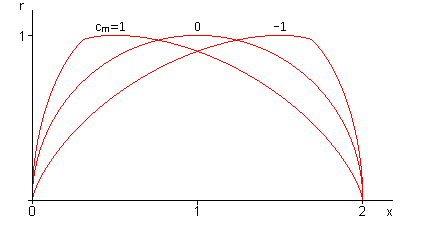
Рис 2. Образующие каплевидных тел ()

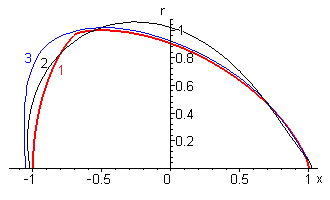
Рис 3. Приближение каплевидного тела (1 – исходное тело, 2 – линейная зависимость от , 3 – квадратичная зависимость )

Литература

1. Короткин А. И. Присоединенные массы судостроительных конструкций. СПб.: Мор вест, 2007. 448 с.

2. Мирошин Р. Н., Халидов И. А. Локальные методы в механике сплошных сред. СПб.: Изд-во С.-Петербургского университета, 2002. 304 с.

3. Ламб Г. Гидродинамика. М.-Л.: ГИТТЛ, 1947. 928 с.

4. Kaplan C. Potential flow about elongated bodies of revolution. NACA Rep., 1936. P. 189–208. http://naca.central.cranfield.ac.uk/reports/1936/naca-report-516.pdf