МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

ПРИ РЕШЕНИИ ПРИКЛАДНЫХ ЗАДАЧ

Антонова Е.А., Данилов А.М.

Пензенский государственный университет архитектуры и строительства

Математическое моделирование позволяет исследовать процессы с различным физическим содержанием. Оно успешно применяется и в самой математике (численные решения - модели истинных решений (реальных объектов)). Однако сложность и многообразие процессов функционирования реальных систем не позволяют получить абсолютно адекватные математические модели. Так как нельзя указать формальные правила для выбора характеристик состояний и параметров исследуемых реальных систем, то исследователь вынужден руководствоваться лишь собственной интуицией, опирающейся на постановку прикладной задачи и понимание природы функционирования системы. Действительно, рассмотрим устройство, которое по числу на входе выдает на выходе число (таблица умножения на 9). Пусть требуется построить математическую модель этого устройства (определить структуру и параметры «черного ящика», преобразующего в ). 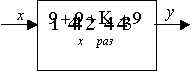Очевидно, задача не имеет однозначного решения; возможны и другие решения, например, со структурными схемами на рис.1 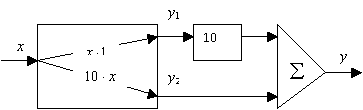(а,б).

а) б)

Рис.1

Если реальная система описывается обыкновенным дифференциальным уравнением с постоянными коэффициентами (входное воздействие преобразуется в выходное ), то решается обратная задача теории дифференциальных уравнений, а именно: по известному решению при заданном определяются коэффициенты дифференциального уравнения:

.

При решении многих технико-экономических экстремальных задач (определение состава композиционного материала, обеспечивающего оптимальные характеристики; определение оптимальных условий культивирования микроорганизмов; управление трудовыми ресурсами и запасами, оптимальное размещение объектов, составление календарных планов, выбор наилучших проектных решений и т.д.) для описания функций отклика (параметры оптимизации) аналитическими зависимостями эффективно используются методы математического планирования эксперимента. Важную роль математические модели играют и при решении задач прокладки систем тепло-, газо-и водоснабжения, трассировки дорог (в основном, используются математическое программирование, теория графов и др. ). При решении задач диагностики отказов (в том числе диагностики заболеваний человека), экспертизы зданий и сооружений широко используются как детерминированные, так и стохастические модели. В качестве иллюстрации рассмотрим использование математического моделирования для коррекции близорукости (дальнозоркости) смещением фокуса нанесением надрезов на роговице (ниже хрусталика), уменьшающими ее упругие характеристики. Вследствие этого роговица изменяет форму под воздействием на нее сил (атмосферное давление, внутриглазное давление, давление век и т.д.). Для прогнозирования смещения в зависимости от параметров надрезов и используется математическое моделирование.

При справедливости гипотезы осевой симметрии роговицы меридиональные сечения роговицы будут идентичны (упругая модель на рис. 2). Кусочно-линейная аппроксимация радиуса кривизны на участке дает , 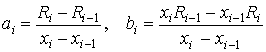(радиус кривизны определяется рефрактомером).

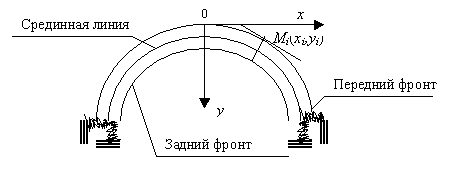
Рис.2

Передний фронт роговицы определится как решение задачи Коши

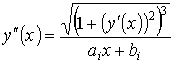
при начальных условиях

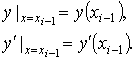
Координаты точек, лежащих на заднем фронте роговой оболочки, приближенно определяются с использованием корнеометра (по значениям толщины роговицы в точках переднего фронта). Далее без затруднений методом наименьших квадратов определяется уравнение заднего фронта оболочки; по уравнениям фронтов - срединная линия меридионального сечения роговицы.

При оптимизации свойств материалов наиболее перспективными на сегодня остаются методы математического планирования эксперимента. При решении многих задач строительного материаловедения наиболее эффективными оказались градиентные методы Франка-Вулфа и штрафных функций [1]. Имеется положительный опыт определения параметров управляющих воздействий человека-оператора по данным нормальной эксплуатации, а также установлению их связи с техническими характеристиками объекта.

Литература

1. Данилов А.М., Гарькина И.А., Домке Э.Р. Математическое и компьютерное моделирование сложных систем. - Пенза: ПГУАС, 2011. -296 с.