АНАЛИТИЧЕСКИЕ МЕТОДЫ

В МОНИТОРИНГЕ СЛОЖНЫХ КОНСТРУКЦИЙ

Пчелинцев И.А., Данилов А.М.

Пензенский государственный университет архитектуры и строительства

Обычно используются как временной, так и частотный способы представления сигнала. Для перехода к частотному способу используется преобразование Фурье:

,

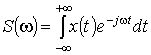- спектральная функция или спектральная плотность (комплексная функция; имеет размерность сигнала, умноженную на время; - спектр амплитуд, - спектр фаз). Функция представляется в виде суммы бесконечного ряда гармонических составляющих с амплитудами 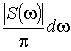, непрерывно заполняющими интервал частот от 0 до , и начальными фазами . Представление дает возможность установить физический смысл .

При мониторинге сложных конструкций используются анализаторы спектров, важнейшей характеристикой которых является разрешающая способность (наименьший интервал по частоте между двумя спектральными линиями, которые ещё разделяются анализатором спектра). Истинный спектр можно получить лишь тогда, когда анализируемое колебание периодично, либо существует только в пределах интервала . Анализатор позволяет получить не истинный спектр 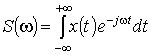, а лишь его оценку 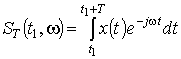(зависит от и ; оценка определяет текущий спектр). Однако следует помнить, что установление точности определения спектра требует знания точного спектра.

По заданному частотному спектру можно определить временную форму сигнала 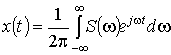. В отличие от спектрального описания детерминированных функций спектральное описание случайного процесса проводится для его статистической характеристики — автокорреляционной функции . Во многих случаях возможна аппроксимация автокорреляционных функций экспоненциальными или экспоненциально-косинусными выражениями:

,	(1)
;	(2)

спектральные плотности соответственно имеют вид:

,

.

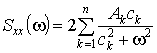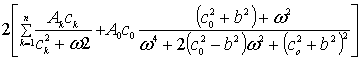При аппроксимации автокорреляционной функции случайного процесса можно воспользоваться нижеприводимым алгоритмом.

1. Выбрать число в выражении (1), исходя из допустимой сложности (1) и ожидаемой точности аппроксимации (эти соображения альтернативны, так как с ростом одновременно растет сложность и точность аппроксимации; во многих случаях удается ограничиться ).

2. Выбрать подходящее значение в выражении (1) так, чтобы функция стремилась к нулю приблизительно с такой же скоростью, как и .

3. Из условия

определить значения функций .

4. Используя функции , определить (для этой цели интегралы заменяются суммами , где - дискретные значения и , - шаг по ).

5. Представить автокорреляционную функцию в виде суммы

.

6. Привести подобные члены и автокорреляционную функцию представить в виде

.

Когда автокорреляционная функция имеет вид (2), описанным выше методом аппроксимируется

.

Приведенный алгоритм прошел практическую апробацию при оценке сохранения работоспособности оборудования мобильных систем при воздействии удара и сопровождающей вибрации [1], а также при разработке обучающих комплексов для различных отраслей промышленности [2,3].

Литература

1. Данилов А.М., Гарькина И.А., Гарькин И.Н. Защита от удара и сопровождающей вибрации: экспоненциально-тригонометрическая аппроксимация функций / Региональная архитектура и строительство. – 2012. –№3(14). – С.85-89.

2. Andreev A.N., Danilov A.M., Klyuev B.V., Lapshin E.V., Blinov A.V., Yurkov N.K. Information models for designing conceptual broad-profile flight simulators / Measurement Techniques. August 2000. – Vol.43. Issue 8. – P.667-672.

3. Данилов А.М., Гарькина И.А., Домке Э.Р. Математическое и компьютерное моделирование сложных систем. – Пенза: ПГУАС. – 2011. – 296 с.