СТОХАСТИЧЕСКИЕ МОДЕЛИ

при решении экономических задач

Хнаев О.А., Гарькина И.А.

Пензенский государственный университет архитектуры и строительства

В последние годы стохастические модели широко используются при решении экономических задач. Это, прежде всего, решаемые методами математического программирования задачи со случайными параметрами (предмет стохастического программирования). В некоторых случаях при решении стохастических задач случайные величины еще до начала решения задачи заменяются усредненными значениями. Однако такой прием (когда случайный процесс заменяется его детерминированной моделью) дает хорошие результаты только тогда, когда рассматриваемая система состоит из достаточно многочисленных объектов и когда случайные отклонения каждого из них взаимно компенсируются. Принятый подход к решению стохастических задач состоит в том, что оптимизируется не сама функция цели, а ее математическое ожидание. Одним из основных подходов к решению таких задач является представление задачи в форме, позволяющей использовать методы нелинейного или динамического программирования.

Не останавливаясь на одношаговых задачах, рассмотрим сразу многошаговые. Они возникают тогда, когда управляемый процесс не полностью определяется начальным состоянием системы и выбранным управлением, а в значительной степени зависит от случая, например, если нельзя точно определить состояние системы на каждом этапе или если переменные, характеризующие состояние системы, являются случайными величинами с известными законами распределения. Так, к стохастической многошаговой задаче приводится задача планирования на длительный период, когда нельзя точно указать значения всех нормативов и коэффициентов, так как они могут измениться под влиянием непредвиденных причин. Особую актуальность решения этих задач приобретают в условиях неустойчивого финансового рынка. Проиллюстрируем их решение на следующем примере. Рантье вложил финансовые средства на счета двух финансовых компаний в сумме и рублей на условиях ежемесячного начисления процентов. Проценты прибыли в расчете на 1 месяц в этих компаниях соответственно равняются и . Предполагая, что расчетные надежности работы компаний составляют и (соответственно вероятности банкротств – ,), определить такую последовательность ежемесячного снятия прибыли со вкладов на счетах финансовых компаний, которая обеспечила бы максимальную ожидаемую прибыль в течение трех месяцев.

Нетрудно убедиться, что рассматриваемая задача сводится к задаче стохастического динамического программирования. Максимальная ожидаемая прибыль в первом месяце (в конце первого этапа) с учетом вероятностей надежной работы компаний составит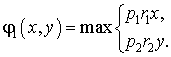

В течение месяца ожидаемая прибыль

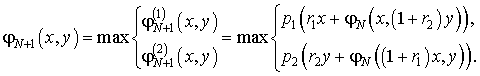
То есть получено функциональное уравнение Беллмана.

Максимальная ожидаемая прибыль в течение трех месяцев будет равна

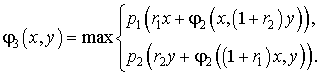
Легко определится оптимальная стратегия рантье по ежемесячному снятию процентов со вкладов.

Примем млн. руб.

Имеем

;

;

;

;

;

.

Так что:

;

;

.

( млн.руб.).

Поскольку , для получения максимальной прибыли после первого этапа (через 1 месяц) проценты следует снять из первой компании. При этом максимум достигается при , то есть когда на втором этапе (через 2 месяца) проценты снимаются из второй компании.

Из предыдущего следует, что значение достигается при , то есть на третьем этапе (через 3 месяца) проценты надо снять из второй компании.

Таким образом, ожидаемая максимальная прибыль рантье в течение трех месяцев составит 313560 рублей при соблюдении им оптимальной стратегии ежемесячного снятия прибыли последовательно со счетов первой, второй, второй компаний. В случае, когда в течение трех месяцев не произойдет банкротств компаний, то фактическая прибыль при выбранной стратегии будет больше ожидаемой и составит:

рублей;

рублей, рублей, рублей,

рублей.

Предлагаемая методика применима и в случае, когда и есть функции времени.