Перспективные методы СИНТЕЗА

композиционных материалов

НА ОСНОВЕ ХАРАКТЕРИСТИК КИНЕТИЧЕСКИХ ПРОЦЕССОВ

Сухов Я.И., Гарькина И.А.

Пензенский государственный университет архитектуры и строительства

Приводятся результаты оптимального синтеза композиционных строительных материалов для защиты от ионизирующих излучений на основе теории оптимального управления с использованием специально построенных по характеристикам кинетических процессов функционалов для оценки их качества.

Существует следующая принятая последовательность этапов для решения технической задачи:

1. Техническая постановка задачи и выбор технического критерия оптимизации.

2. На основе технической постановки задачи строится математическая модель объекта управления в форме системы операторных уравнений (дифференциальных, интегральных, разностных, дифференциально-разностных, дифференциально-интегральных и т.д.)

Математическая модель и пути ее построения зависят от степени изученности объекта, наличия опыта разработки аналогичных систем, полноты знания физических процессов, характеризующих поведение объекта, и осуществляется на основе теоретических исследований по изучению физических процессов в системе, логического анализа, идентификации по данным нормальной эксплуатации и т.д. Далее делается оценка области применения математических моделей. Здесь же выбираются компоненты вектора управления, параметры системы и возмущения. Устанавливаются фазовые координаты и строится пространство состояния объекта.

При разработке оптимальных систем указываются ограничения на компоненты вектора управления и фазовые координаты.

Так, ограничения на фазовые координаты могут дать принадлежность вектора состояния некоторому замкнутому множеству точек n-мерного пространства. Они могут определять прочность, жесткость объекта и т.д. Здесь же указываются ограничения на вектор управления (например, энергопотребление).

На этом же этапе определяются начальные или краевые условия, осуществляется выбор критерия для оценки качества управления.

3. В предположении полной формализации задачи выбирается метод оптимизации. Как правило, предполагается задание математической модели объекта применительно к выбранному методу на его языке. Однако не исключается, когда модель подгоняется под выбранный метод оптимизации. Например, по системе дифференциальных уравнений линейного объекта может быть построен соответствующий функционал качества на основе корней характеристического полинома.

4. Выбор численных методов, реализующих метод оптимизации: методов решения систем дифференциальных уравнений, определения значений функционала качества и т.д.

5. Разработка и отладка программ для решения задачи оптимизации на ЭВМ, не исключая корректировку численных методов для повышения точности и вычислительной эффективности алгоритма.

6. Анализ полученных результатов оптимизации с возможной корректировкой и упрощением, как всей математической задачи, так и отдельных ее элементов. Результаты решения математической задачи являются исходной информацией для уточнения формулировки технической задачи, и итерационный процесс может повторяться до достижения заданной точности.

Практически без оговорок указанная последовательность может использоваться при синтезе материалов из условий получения требуемых кинетических процессов формирования физико-химических характеристик материалов (прочность, твердость, параметры тепловыделения, химическая стойкость и т.д.). При этом основные понятия и определения материаловедения легко интерпретируются в соответствующих терминах, принятых в теории систем управления (управляемость, наблюдаемость и идентифицируемость и т.д.).

Синтез материалов осуществлялся по функционалам качества, схожим используемым при синтезе тренажеров для аэрокосмической отрасли с оценкой их качества по шкале Купера-Харпера. Качество материала оценивался по характеристикам кинетических процессов как функций времени. Оптимизация структуры и свойств материала производилась на основе выбора параметров кинетических процессов формирования его физико-механических характеристик (радиационной стойкости, набора прочности, тепловыделения, усадки и др.), описывающихся обыкновенными дифференциальными уравнениями. Функционал качества принимался в виде

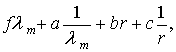
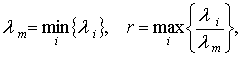
где (-l_i ) – корни характеристического полинома, l_i>0, i = ; f, a , b, c – весовые константы. Качество материала тем выше, чем меньше . При решении задачи использовались области равных оценок качества материала d_k-1 £ < d_k, где k – класс системы; ; N - балльность шкалы. Характеристики ингредиентов и материала в целом определялись градиентными методами.

Эффективность предложенной методики подтвердилась при синтезе строительных материалов со специальными свойствами [1,2].

Литература

1. Гарькина И.А., Данилов А.М. Приложения теории систем к управлению структурой и свойствами композитов / Вестник СибАДИ, – 2013. – №5(33). –С.58-63.

2. Гарькина И.А., Данилов А.М. Управление качеством материалов со специальными свойствами // Проблемы управления. – 2008. – № 6. – С. 67-74.