Физика/1. Теоретическая физика

К.т.н. Хайдаров Г.Г., к.т.н. Хайдаров А.Г.

Санкт-Петербургский государственный технологический институт (технический университет), Россия

Современное представление о физической природе поверхностного натяжения жидкости

Физическое понятие поверхностного натяжения жидкости до некоторого времени оставалось в тени крупных достижений в областях физической химии и молекулярной физики. Так Я. Френкель еще в начале 20 века предполагал наличие определенной связи коэффициента поверхностного натяжения с другими физическими величинами. И. Ленгмюр (Langmuir I.) указал на некую производную от энтальпии, но уточнять ее не стал. В настоящее время концепции, основанные на геометрическом моделировании испарения вещества, объяснили физическую природу поверхностного натяжения. Таким образом, доказана суть поверхностного натяжения, как части внутренней энергии вещества. Далее кратко изложена данная концепция и её развитие.

К данным концепциям относятся: теоретическая модель «распаковки», опубликованная Г. Г. Хайдаровым в 1983 году [1] с теоретическим выводом расчетной формулы. Другой теоретической моделью является концепция «салями метода», опубликованная академиком Виктором Ф. Вайскопфом (Victor F. Weisskopf) в 1985 году [2,3]. В дальнейшем аналогичные теоретические модели опубликованы рядом авторов с выводом аналогичных формул. Например [4, 5].

Теоретические модели «распаковки» 1983 года и «салями метода» 1985 года базируются на одинаковом принципе геометрического моделирования физического явления. В первом грубом приближении можно сформулировать модель «распаковки» так. При испарении молекул вещества происходит разрыв связей каждой молекулы с соседними молекулами вещества по всем шести направлениям осей координат (х, -x, y, -y, z, -z) с дальнейшим перемешиванием молекул в объеме газа, а при изучении поверхностного натяжения молекул вещества происходит разрыв связей по одному из шести направлений, перпендикулярному поверхности разрыва. Или так. Внутренняя энергия характеризует шесть разрывов по осям координат (х, -x, y, -y, z, -z), а поверхностное натяжение характеризует один разрыв – «распаковку».

Разница двух вышесказанных концепций состоит лишь в геометрических интерпретациях процессов испарения (и поверхностного натяжения) и в областях применения данных теоретических исследований. В теории «распаковки» 1983 года [1] в отличие от «салями метода», кроме общей концепции была еще опубликована конечная формула для расчета поверхностного натяжения для веществ, подтвержденная справочными данными для 64 веществ в диапазоне температур от -253 до +200 градусов Цельсия. В первом приближении (при соблюдении закономерности Менделеева - Клапейрона) формулу для определения коэффициента поверхностного натяжения жидкости можно записать через удельную теплоту парообразования как:

251658240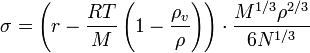Описание: \sigma= \left(r - \frac{R T}{M} \left(1-\frac{\rho_v}{\rho} \right) \right)\cdot \frac{M^{1/3} \rho^{2/3}}{6 N^{1/3}}                                       (1)

или через внутреннюю энергию U, как:

251658240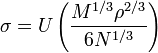Описание: \sigma= U \left(\frac{M^{1/3}\rho^{2/3}}{6 N^{1/3}}\right)                                                                      (2)

где r – теплота парообразования, Дж/кг;  251658240Описание: \rho – плотность жидкости, кг/ м3;  251658240Описание: \rho_v –плотность пара, кг/ м3; R– универсальная газовая постоянная, Дж/(кмоль * K); T– температура, K; U – внутренняя энергия жидкости, Дж/кг; M – молекулярная масса, кг/кмоль; N – число Авогадро, кмоль-1.

Справедливость формулы (1) определялась по расчетному значению коэффициента эффективности молекул, равного отношению эффективного радиуса реальной молекулы к теоретическому радиусу симметричной сферической молекулы.

251658240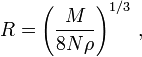Описание: R = \left(\frac{M}{8 N \rho}\right)^{1/3} \, ,

251658240Описание: R_e = R\cdot n, где n – коэффициент эффективности молекулы

В результате расчетов для молекул, близких по форме к симметричной сферической форме, коэффициент n должен быть равен единице.  Обработка  справочных данных теплофизических свойств для большинства веществ подтвердила теоретические формулы с погрешностью до 15%. Для части веществ с асимметричной формой коэффициент эффективности молекулы отличается от единицы.

Дальнейшее развитие модели «распаковки» в 2010-2012 годах показало применимость данной концепции «распаковки» для теоретического объяснения зависимостей, известных в физике и физической химии.

Так следствием данной модели является хорошее согласование с молекулярно-кинетической теорией идеальных газов. А именно, теоретический вывод взаимосвязи значений теплоемкостей для одно-, двух- и трехатомных газов. Доказано влияние пространственного расположения атомов на значение теплоемкости молекулы [6].

Другим следствием данной модели «распаковки» является теоретический вывод эмпирической формулы для определения влияния температуры на поверхностное натяжение. Формула хорошо согласуется с широко известной эмпирической зависимостью – правилом Этвёша ( Eötvös rule ). Теоретически выведены значения эмпирических коэффициентов пропорциональности [7]. Формула  была проверена по данным из справочника по теплофизическим свойствам газов и жидкостей.

Кроме того были произведены расчеты по формулам (1), (2) по данным из справочника для металлов. Результаты подтвердили применимость концепции «распаковки» до верхней границы температу в 1100 градусов Кельвина [7].

Более подробную информацию о теории «распаковки» и ее следствиях можно прочитать в свободном доступе интернета в википедии ( ru.wikipedia.org ) и в викиучебнике ( ru.wikibooks.org ) на русском языке, набрав «Поверхностное натяжение».

Литература:

1.     Г.Г. Хайдаров  О связи поверхностного натяжения с теплотой парообразования // Журнал физической химии. 1983, № 10, с. 2528-2530

2.     Weisskopf V. F. Search for simplicity // Am. J. Phys. 1985. Vol. 53. N 1. P. 19–20.

3.     Weisskopf V. F. Search for simplicity: the size of molecules revisited // Am. J. Phys. 1985. Vol. 53. N 7. P. 618–619.

4.     Garai J. Physical model for vaporization // Fluid Phase Equilibria. 2009. Vol. 183. P. 89–92.

5.     Матюхин С. И., Фроленков К. Ю., Антонов О. Н., Игошин В. М. Плёнки и покрытия // Труды 6-й междунар. конф. «Плёнки и покрытия». СПб., 2001. C. 577–581. . 2010. № 1. C. 111–113.

6.     Хайдаров Г.Г., Хайдаров А.Г., Машек А. Ч. Физическая природа поверхностного натяжения жидкости // Вестник Санкт-Петербургского университета. Серия 4 (Физика, химия). 2011. Выпуск 1. с.3-8

7.     Хайдаров Г.Г., Хайдаров А.Г., Машек А. Ч. Майоров Е.Е. Влияние температуры на поверхностное натяжение // Вестник Санкт-Петербургского университета. Серия 4. 2012. Выпуск 1. с.24-28