Технические науки/10. Горное дело

Низаметдинов Ф.К., Оленюк С.П., Бахтыбаева А.С.

Карагандинский государственный технический университет

Особенности проектирования схемы наблюдения для автоматизированного мониторинга сдвижений приконтурного массива горных пород

Вопрос сдвижения горных пород остаётся актуальным на протяжении всей истории развития горного дела. Так от успешного решения проблем управления горным давлением и процессом сдвижения горных пород, при разработке месторождений полезных ископаемых, зависит не только их экономическая эффективность и сохранность объектов, попавших в зону влияния горных работ, но и безопасность самих работ.

Источником данных о геомеханическом состоянии массива горных пород и его изменении во времени являются инструментальные измерения сдвижений и деформаций, выполняемые по специально оборудованным наблюдательным станциям (рисунок 1).

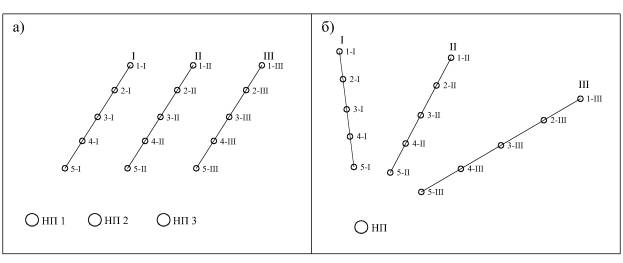
Рисунок 1 – схемы наблюдательных станций

При этом пункт наблюдения принято располагать в створе наблюдательной линии. В случае параллельного размещения наблюдательных линий, число наблюдательных пунктов должно им соответствовать (рисунок 1, а), снижает эффективность работ. Радиальное положение наблюдательных линий позволяет использовать один наблюдательный пункт, но при этом увеличивается неравномерность положения реперов.

Схемы подобных наблюдательных станций изначально были разработаны для методик инструментальных наблюдений уже устаревшими приборами и удобства “ручной” камеральной обработки результатов измерений. Репера в таких схемах формируют нерегулярную и неоднородную по плотности сеть.

Полученные при этом данные, как правило, характеризуют продольные и поперечные смещения в плоскости наблюдательных линий, что затрудняет их взаимный анализ на площади всего исследуемого участка.

Однако необходимость такого анализа очевидна в случае сложных конфигураций породных обнажений и неравномерном действии сил, особенно при совмещении открытого и подземного способа разработки полезных ископаемых.

Оптимальной схемой расстановки реперов, обеспечивающей взаимную увязку и анализ данных, полученных по каждому из реперов, является триангуляционная сеть – основа современного моделирования трёхмерных поверхностей (Рисунок 2).

В процессе проектирование триангуляционной сети реперов получают их проектные координаты, опираясь на данные топографии, тригонометрической съёмки и прогноза возможных сдвижений, соблюдая следующие условия:

· Максимальный и равномерный охват области возможных сдвижений;

· Размещение реперов в характерных точках поверхности;

· Максимизация минимального угла в треугольниках сети;

· Условие триангуляции Делоне – внутри описанных вокруг каждого треугольника сети окружностей не должно быть иных точек сети.

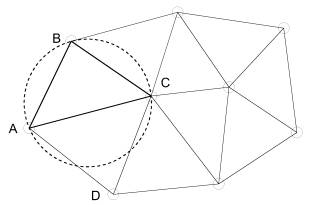
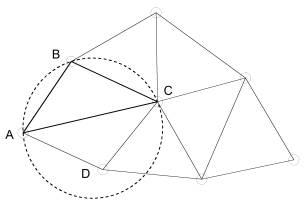
I) II)

Рисунок 2 – схемы триангуляционных сетей реперов

На рисунке 2 сеть I соответствует критерию Делоне, а сеть II – не соответствует, так как репер “D” попадает в окружность, описанную вокруг треугольника ABC.

Выполнение условия триангуляции Делоне обеспечивает оптимальную конфигурацию сети для решения поставленных задач.

Вынос на местность проекта сети будет осуществляться по заданным координатам с помощью системы GPS, а измерения – стационарно установленным роботизированным тахеометром в автоматическом режиме.

Автоматическая система мониторинга позволит эффективно использовать преимущества триангуляционной сети для комплексного исследования геомеханических процессов в массиве горных пород на всей площади сети.

Список использованных источников

1 Методические указания по наблюдениям за деформациями бортов, откосов уступов и отвалов на карьерах и разработке мероприятий по обеспечению их устойчивости. Приказ Комитета по государственному контролю за чрезвычайными ситуациями и промышленной безопасностью Республики Казахстан от «22» сентября 2008 года № 39.

2 Скворцов А. В. Триангуляция Делоне и её применение. Томск: Изд-во Томского университета, 2002. 128 с.