Доповідь/Технічні науки – Автоматизовані системи управління на виробництві

УДК 681.513:622.24

Д.т.н. Семенцов Г.Н., Кизима Л.В.

Івано-Франківський національний технічний університет нафти і газу

Експериментальні оцінки статистичних характеристик флуктуацій осьового навантаження на долото в системі керування процесом буріння нафтових і газових свердловин

Технологічний процес буріння нафтових і газових свердловин є випадковим нелінійним невідтворюваним параметрично невизначеним об’єктом керування, що функціонує за умов апріорі невідомих зовнішніх збурень. Тому параметри режимів буріння (осьове навантаження (осьова сила) на долото F і швидкість обертання долота n) і їх взаємозв’язки з показниками процесу визначаються ймовірнісними і статистичними характеристиками, а саме – оцінками математичного сподівання, дисперсії, спектральної густини та автокореляційної функціЇ [1].

Проте до сьогодні не вирішене питання контролю осьової сили на долото безпосередньо на вибої свердловини і тому цей параметр, який визначає режим буріння, обчислюється за формулою [2]:

, (1)

де G – вага колони бурильних труб, яка вільно висить на гаку бурової установки;

G₁ – вага колони бурильних труб на гаку під час буріння ;

G_γ – втрата ваги від зміни густини промивальної рідини;

G_T – сили тертя бурильних труб об стінки свердловини.

Розробка засобів вимірювання осьової сили на долото під час буріння нафтових і газових свердловин є актуальною науково-технічною задачею у зв’язку з інтенсивним впровадженням в даний час автоматизованих систем керування режимами буріння [3].

Проте, аналіз літературних джерел [2, 3 та ін.] показує недостатній об’єм проведених досліджень в контексті розробки ефективних вимірювальних каналів для контролю осьової сили на долото, яка є основним параметром керування процесом буріння. Особливо важливим цей параметр є для вирішення задач оптимального керування, коли треба вибрати ефективне зусилля на породу вибою з урахуванням типу долота, глибини свердловини, фізико-механічних і абразивних властивостей породи та інших факторів, що впливають на показники технологічного процесу буріння.

Тому метою даної роботи є аналіз статистичних характеристик флуктуацій осьової сили на долото, за результатами, що отримані під час експлуатації давача, розробленого на кафедрі автоматизації технологічних процесів і моніторингу екології Івано-Франківсього національного технічного університету нафти і газу.

Для вимірювання осьової сили на долото використовується ресорний давач ваги колони бурильних труб типу ДВР-2б, первинний вимірювальний перетворювач, який перетворює натяг канату у кут повороту сельсину-давача типу БД-404А. Разом з сельсином-приймачем і двигуном вони створюють стежну систему, яка передає сигнал, пропорційний переміщенню, на вихід, до якого приєднується реєструючий прилад. Довжина лінії зв’язку дорівнює ≈ 100м. Обчислення осьової сили на долото здійснюється пристроєм згідно формули (1).

Для дослідження статистичних характеристик флуктуацій осьової сили на долото використані результати вимірювань, що були отримані [4] при бурінні свердловини № 1-Синьовидне долотом III У 295,3 СЗГ на глибині 4666,5-4681,7 м із застосуванням установки «Уралмаш-4Е». Умови буріння: середня осьова сила на долото F=50 kH, частота обертання ротора Q=, густина бурового розчину , порода – аргіліти бистрицької світи.

Розрахунок статистичних характеристик вихідних даних у вигляді 205 одиниць випадкового сигналу проведений за допомогою програмних продуктів MathCad, Curve Expert Pro v.1.63, Matlab.

Графіки зміни осьової сили в часі, отримані в результаті обробки експериментальних даних в програмі MathCad, наведено на рис. 1.

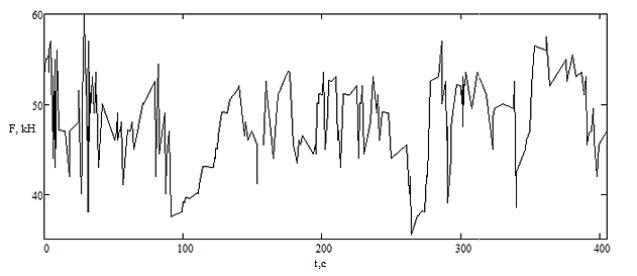
Рисунок 1 – Графік зміни осьової сили у часі, отриманий в результаті обробки експериментальних даних в програмі MathCad

За допомогою середовища MathCad отримали наступні оцінки випадкового процесу F(t) (в розрахунках позначення сили F замінимо на K).

– Математичне сподівання : m=mean(K), mean(K)=47.929,

– Дисперсія: зміщена оцінка – var(K)=24.581,

не зміщена оцінка – var(K)=24.702,

– Середнє квадратичне відхилення: зміщена оцінка – stdev(K)=4.958,

незміщена оцінка – stdev(K)=4.97.

Ці характеристики для кожного конкретного моменту є середніми з множини. Вони визначаються одномірним законом розподілу. Для визначення закону розподілу і його перевірки за допомогою критерію Пірсона поділимо вибірку n=205 значень осьової сили на долото F на інтервали та визначимо їх абсолютні та відносні частоти. Впорядковуємо досліджувану вибірку у порядку зростання. Для цього застосуємо наступну функцію пакету MathCad:

.

Отримуємо таблицю значень:

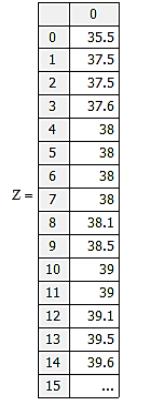
Знаходимо зону розсіювання значень за формулою:

R=max(x)-min(x),

R=24.5.

Розділюємо її на 7 груп із інтервалами h=3.5. Далі визначаємо границі інтервалів та зберігаємо їх як масив int:

,

де Z₀ – найменше значення величини х,

int₀ – нижня границя першого інтервалу,

int_i+1 – верхня границя і-го інтервалу.

Середини інтервалів розрахуємо за формулою:

.

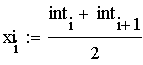Для обчислення абсолютних частот інтервалів (масив mi) використаємо вбудовану функцію MathCad:

mi:=hist(int,Z).

Відносні частоти обчислюємо за формулою:

.

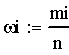У результаті розрахунків отримаємо наступні значення:

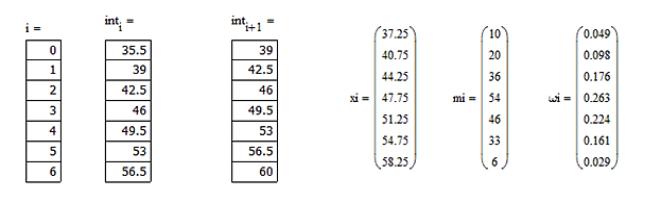
Таблиця 1

Сортування масиву експериментальних значень осьової сили на долото F

Кількість інтервалів	Межі інтервалів		Кількість повторень	Середнє значення	Імовірність
	від	до
0	35.5	39	10	37.25	0.049
1	39	42.5	20	40.75	0.098
2	42.5	46	36	44.25	0.176
3	46	49.5	54	47.75	0.263
4	49.5	53	46	51.25	0.224
5	53	56.5	33	54.75	0.161
6	56.5	60	6	58.25	0.029

Виконаємо перевірку обчислення абсолютних та відносних частот:

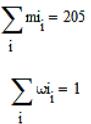
За отриманими даними побудуємо гістограму густини відносних частот, яка зображена на рис 2.

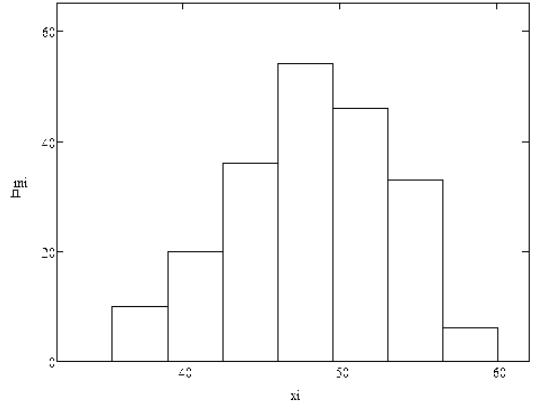
Рисунок 2 – Гістограма густини відносних частот для осьової сили на долото F

По отриманій гістограмі можна припустити, що даний розподіл підпорядковується нормальному закону.

Для підтвердження даної гіпотези скористаємось критерієм Пірсона:

.

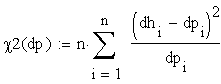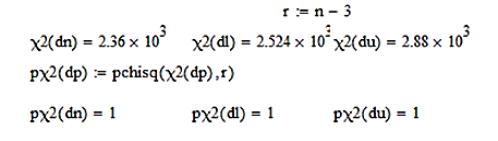
Отже, даний розподіл (рис. 2) підпорядковується закону Гауса.

Для випадкової функції F(t) отримані на основі нього характеристики, такі як оцінка математичного сподівання та дисперсія, ще не є достатніми для оцінки характеру протікання випадкового процесу в часі. Тому необхідно ще встановити зв’язок між значеннями випадкового процесу F(t) в різні моменти часу. Це зробимо за допомогою двохмірної функції розподілу [1] – автокореляційної функції або функції спектральної густини.

Для визначення автокореляційної функції скористаємось пакетом Matlab. Імпортуємо дані і отримаємо графічне зображення нормованої автокореляційної функції осьовоїсили на долото R_xx(τ) на рис. 3.

>> R_xx =xcorr(F,T,205)

>> plot(R_xx)

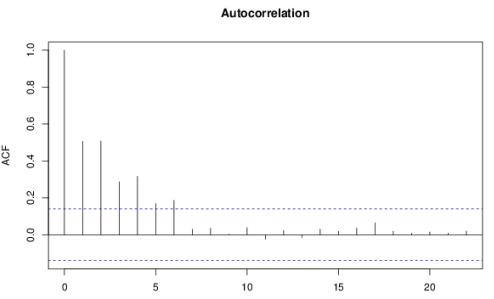
Рисунок 3 – Графічне зображення aвтокореляційної функції для осьової сили на долото F

Графік отриманої вто кореляційної функції підтверджує, що досліджуваний процес F(t) є стаціонарним і ергодичним.

Для одержання рівняння вто кореляційної функції скористаємось програмою Curve Expert. Ввівши значення, які були розраховані, отримую різні рівняння з різними похибками і різними коефіцієнтами кореляції. Проаналізувавши всі рівняння, вибираємо рівняння Exponential:

. (2)

Побудуємо графік функції, що описується даним рівнянням (рис. 4 ).

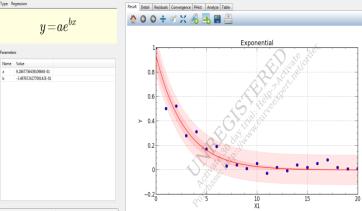
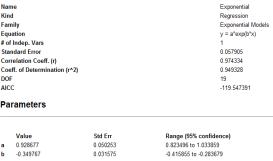
Рисунок 4 – Графічне зображення вто кореляційної функції для осьової сили на долото F при використанні Curve Expert (Exponential)

Як бачимо, графік повністю відтворює вище наведену автокореляційну функцію з коефіцієнтом кореляції r = 0,974 і стандартною похибкою S` = 0,058.

Відзначимо, що при статистичному аналізі стаціонарних випадкових функцій зручно користуватись спектральною густиною випадкової функції, тобто двохстороннім зображенням Фур’є автокореляційної функції:

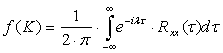, (3)

де R_xx (t) – оригінал автокореляційної функції.

Спектральна густина є додатною функцією у всьому діапазоні частот від 0 до ¥. Вона не містить відомостей про фази окремих гармонійних складових. За допомогою приведеної формули можна визначити спектральну густину по заданій аналітично автокореляційній функції R_xx (t).

Отже, визначимо спектральну густину, використовуючи пакет MathCad на основі автокореляційної функції R_xx(t). Для цього наступним кроком збережемо отримані значення автокореляційної функції в масив даних.

_.

Далі використаємо перетворення Фур’є, взявши за основу вбудовану функцію cfft(x):

_.

Отримане перетворення потрібно взяти по модулю, оскільки спектральна густина є додатною у всьому діапазоні частот. Отже:

i=0..length(z)-1,

a_i=|z_i|,

ω_i=i.

За отриманими даними побудуємо залежність S від w. Так ми отримуємо графік спектральної густини S(w). Модуль значення спектральної густини визначає амплітудно-частотну характеристику сигналу, а її аргумент – фазо-частотну характеристику. АЧХ сигналу являється парною функцією, а ФЧХ – непарною. У загальному вигляді зміст S(w) визначається як амплітуда сигналу, що припадає на 1 Гц в нескінченно вузькій полосі частот, яка включає в себе розглянуту частоту w.

Отже, маємо графік спектральної густини для сигналу F(t) (рис. 5).

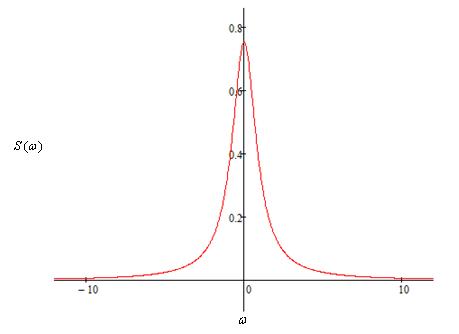
Рисунок 5 – Графік спектральної густини для F(t)

При дослідженні автоматичних систем виникає необхідність створювати типові випадкові впливи штучно – за допомогою спеціальних генераторів. Найпростіше ця задача вирішується з використанням методу формуючого фільтра. Суть методу полягає в тому, що потрібний випадковий сигнал отримується шляхом пропускання білого шуму через фільтр з відповідною частотною характеристикою.

Частотна передавальна функція W_ф(jω) фільтра зв’язана з спектральною густиною S(w) формуючого сигналу наступним співвідношенням [5]:

{W_ф(jω)}²= S(w). (4)

Для пошуку функції W_ф(jω) необхідно розкласти спектральну густину S(w) на спряжені множники W_ф(jω) і W_ф(-jω). З цих двох множників фізично реалізованим у вигляді фільтра є лише перший множник, в якому нулі і полюси (корені чисельника і знаменника) знаходяться у верхній півплощині.

Для сигналу F(t) з експоненціальною кореляційною функцією маємо:

S(w)= (5)

Звідси частотна функція фізично реалізованого фільтра:

W_ф(jω)=

Тоді :

W_ф(jω)= (6)

Побудуємо графік АФХ формуючого фільтру для F(t) в програмі MathCad:

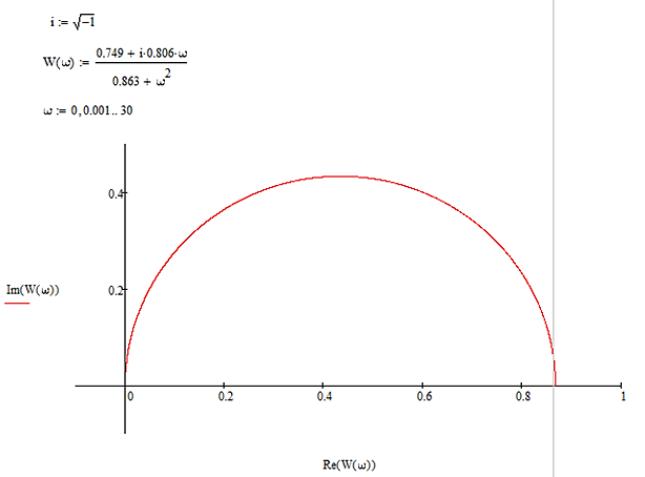
Рисунок 6 – Графік АФХ формуючого фільтру для F(t)

Оскільки оператор бурової установки прагне підтримувати осьову силу на долото постійною з певними флуктуаційними коливаннями, то оцінка математичного сподівання на таких ділянках постійна, а реалізація функції осьової сили на долото має вигляд квазістаціонарної випадкової функції.

Висновок

Проведений аналіз довів, що функція F(t) має властивості ергодичності як по відношенню до математичного

сподівання, так і автокореляційної функції, що дозволяє досліджувати її статистичні характеристики на основі реалізації, що має обмежену довжину. Спектральна густина сигналу F(t) дозволила визначити амплітудно-фазову характеристику формуючого фільтру.

Література:

1. Волгин В.В. Оценка корреляционных функцій в промышленных системах управления / В.В.Волгин, Р.Н.Каримов. – М.:Энергия,. – 80 с.

2. Семенцов Г.Н. Автоматизація технологічних процесів у нафтовій та газовій промисловості: [навч. посібник] / Г.Н.Семенцов, Я.Р.Когуч, Я.В.Куровець, М.М.Дранчук. – Івано-Франківськ: ІФНТУНГ, 2009. – 300 с.

3. Оганов Г.С. Динамический аналіз процесса углубления скважин / Г.С.Оганов, С.А.Ширин-Заде, А.А.Парамонов // Вестник Ассоциации бурових подрядчиков, № 1, 2009. – С. 40-44.

4. Семенцов Г.Н. Автоматизація процесу буріння свердловин / Г.Н.Семенцов – Івано-Франківськ: ІФНТУНГ, 1999. – 300 с.

5. Семенцов Г.Н. Теорія автоматичного керування: [навч. посібник] / Г.Н.Семенцов – Івано-Франківськ: ІФНТУНГ, 1999. – 611 с.