к.т.н. Литвинов Е.В., Щевелев С.Ю., Цыбулин В.Ю., к.т.н.
Матеев Е.З. д.т.н. Шахов С.В.
Воронежский государственный университет инженерных
технологий, Россия
Моделирование процесса сушки
продуктов
поперечного сечения с
конвективным и СВЧ энергоподводом
Рассматривается процесс сушки частицы в форме параллелепипеда с линейными
размерами ![]() ,
,![]() ,
,![]() ,
причем
,
причем ![]() и
и ![]() (рис. 1).
(рис. 1).
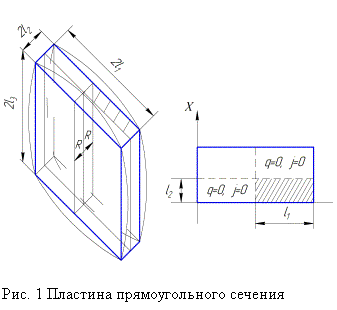 Изменение давления в частице пренебрежимо мало.
Энергоподвод осуществляется конвекцией за счет теплоотдачи от нагретого теплоносителя,
а также, СВЧ-нагрева вследствие сверхвысокочастотной энергии электромагнитного
поля и реализации внутренних тепловых источников.
Изменение давления в частице пренебрежимо мало.
Энергоподвод осуществляется конвекцией за счет теплоотдачи от нагретого теплоносителя,
а также, СВЧ-нагрева вследствие сверхвысокочастотной энергии электромагнитного
поля и реализации внутренних тепловых источников.
Полагаем,
что поля температуры и влагосодержания симметричны относительно серединных
поверхностей. В этом случае можно ограничиться рассмотрением ![]() пластины образца (рис. 1).
пластины образца (рис. 1).
Дифференциальные уравнения тепловлагопереноса в
частице имеют вид:
![]() (1)
(1)
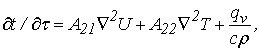 (2)
(2)
где ![]()
![]()
![]()
![]()
![]() коэффициент диффузии влаги в материале;
коэффициент диффузии влаги в материале; ![]() относительный коэффициент термодиффузии;
относительный коэффициент термодиффузии; ![]() теплота конденсации пара;
теплота конденсации пара; ![]() относительный коэффициент диффузии пара;
относительный коэффициент диффузии пара; ![]() коэффициент диффузии пара в материале;
коэффициент диффузии пара в материале; ![]() теплоемкость высушиваемого материала;
теплоемкость высушиваемого материала; ![]() коэффициент температуропроводности материала;
коэффициент температуропроводности материала;
![]() влагосодержание;
влагосодержание; ![]() температура;
температура; ![]() объемная интенсивность внутренних тепловых
источников,
объемная интенсивность внутренних тепловых
источников,
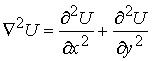 (3)
(3)
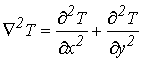 (4)
(4)
Задание
начальных и граничных условий.
Для потенциалов ![]() и
и ![]() граничные условия зададим в
виде граничных условий третьего рода, когда задается потенциал среды окружающей
объект и закон потенциалоотдачи между поверхностью тела и окружающей средой.
граничные условия зададим в
виде граничных условий третьего рода, когда задается потенциал среды окружающей
объект и закон потенциалоотдачи между поверхностью тела и окружающей средой.
В начальный момент времени температура и влагосодержание равномерны по
координатам
![]()
![]()
Граничные условия:
При
![]()
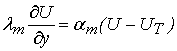 (5)
(5)
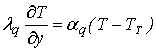 (6)
(6)
При
![]()
![]() (7)
(7)
![]() (8)
(8)
При ![]()
![]() (9)
(9)
![]() (10)
(10)
При ![]()
![]() (11)
(11)
![]() (12)
(12)
Здесь: ![]() коэффициент массопроводности материала;
коэффициент массопроводности материала; ![]() коэффициент теплопроводности;
коэффициент теплопроводности; ![]() коэффициент массоотдачи;
коэффициент массоотдачи; ![]() коэффициент теплоотдачи.
коэффициент теплоотдачи.
Приведем дифференциальные уравнения и условия единственности к
безразмерному виду.
Вводим безразмерные переменные:
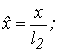
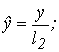
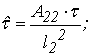
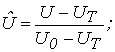
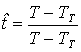
Получим:
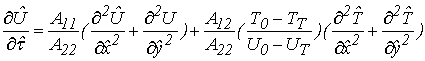 , (13)
, (13)
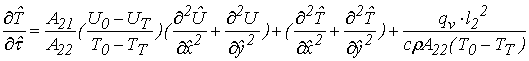 ,(14)
,(14)
Введем
обозначения для безразмерных комплексов, стоящих перед дифференциальными
операторами в правых частях уравнений (13), (14):
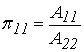 , (15)
, (15)
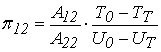 , (16)
, (16)
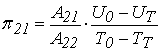 , (17)
, (17)
С учетом выражений для ![]() …
…![]() после преобразований следует:
после преобразований следует:
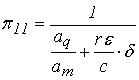 , (18)
, (18)
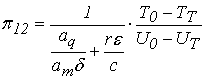 , (19)
, (19)
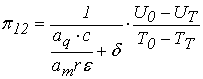 (20)
(20)
Уравнения (13), (14) приобретают вид:
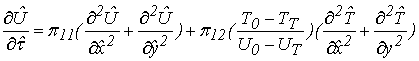 , (21)
, (21)
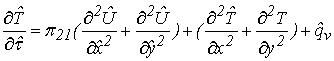 , (22)
, (22)
где 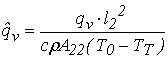 , (23)
, (23)
или безразмерная интенсивность внутренних тепловых
источников.
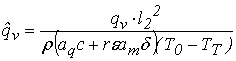 (24)
(24)
Начальные условия:
![]() ; (25)
; (25)
![]() (26)
(26)
Приведем граничные
условия к безразмерному виду.
При ![]()
![]() , (27)
, (27)
![]() (28)
(28)
где 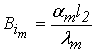 ,
, 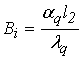 - числа Био, соответственно, для массо- и теплообмена.
- числа Био, соответственно, для массо- и теплообмена.
При ![]()
![]() , (29)
, (29)
![]() (30)
(30)
где ![]() - параметрический критерий (отношение ширины
к высоте частицы).
- параметрический критерий (отношение ширины
к высоте частицы).
При ![]()
![]() , (31)
, (31)
![]() (32)
(32)
При ![]()
![]() , (33)
, (33)
![]() (34)
(34)