УДК 532.517, 663.1, 66.974 Біологічні науки/11.Біоінженерія та біоінформатика

к.т.н. Костик С. І., Ревтов О.О., Сушко А.О.

Національний технічний університет України «КПІ»

Математичне моделювання гідродинаміки при концентруванні мікробіологічних культуральних рідин в роторно-дисковому апараті

На сьогоднішній день технологія концентрування (зневоднення) термолабільних мікробіологічних матеріалів є актуальною проблемою в біотехнологічній, харчовій, фармацевтичній і медичній промисловості [1].

Процес зневоднення термолабільних матеріалів, можливо здійснити в роторно-дисковому плівковому випарної апараті (РДПВА). РДПВА на валу має ряд дискових насадок, які частково занурені в культуральний розчин і приводяться приводом в обертальний рух (рис. 1.) Було поставлено завдання визначити величину наростаючого пограничного шару на поверхні дискової насадки і відповідно градієнти напружень зсуву за допомогою математичного моделювання, що дасть можливість визначення оптимальних робочих параметрів (габаритні розміри диска, швидкість обертання, температура газового теплоносія і т.д.) для реального апарата.

На поверхні плоского диска, що обертається, який частково занурений в культуральну рідину, утворюється тонка рідинна плівка, яка обдувається теплим газовим теплоносієм при виході диска з рідини. З поверхні плівки в теплоносій випаровується волога, при цьому температура розчину, що концентрується не перевищує температуру мокрого термометра. Концентрація розчиненої речовини в рідині підвищується, процес триває до досягнення заданої концентрації.

На процес випаровування вологи з плівки рідини впливає декілька факторів, у тому числі товщина плівки, яка в свою чергу визначається швидкістю обертання диска, фізичними властивостями рідини, габаритними розмірами диска. Для оцінки впливу різних факторів на товщину плівки рідини складаємо математичну модель процесу течії рідини поблизу поверхні частково зануреного диска. Враховуючи геометричну форму диска вибираємо циліндричну систему координат (рис.1 , а). Початок координат поміщаємо на перетин осі обертання з площиною диска. В умовах випаровування води з поверхні плівки, можна припустити, що теплова енергія підводиться до не зануреної частини диска і повністю витрачається на випаровування, при цьому температура розчину залишається постійною, тобто процес течії рідини поблизу поверхні диска відбувається в ізотермічних умовах.

Таким чином математична модель складається з рівнянь Нав'є-Стокса і рівняння нерозривності, система рівнянь (1).

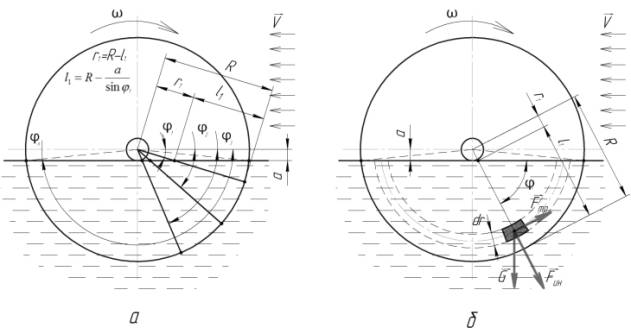
Рис 1. Розрахункова схема обертового диска в потоці теплоносія.

а - основні геометричні розміри елементів диска; б - дія сил інерції F_ін, тертя F_тр і тяжіння G на шар рідини шириною dr.

Запишемо математичну модель процесу з урахуванням прийнятих припущень:

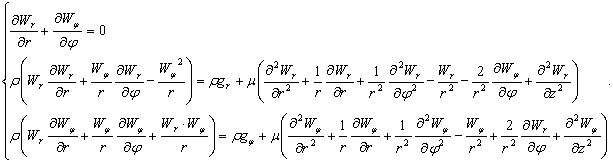(1)

Граничні умови:

(2)

(3)

При сталому режимі роботи обладнання процес течії плівки рідини поблизу поверхні диска визначається дією сил тяжіння, інерції і тертя. В умовах ламінарного руху рідини, швидкість у напрямку осі Z практично відсутня (рис. 1, б).

Після значних перетворень за допомогою пакету MathCad 15 знайдено складові швидкостей по відповідним осям і через вирази для зміни кількості руху був отриманий вираз, який вирішено відносно похідної :

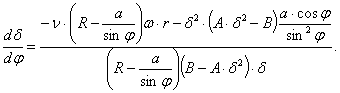(4)

Інтегруємо диференціальне рівняння (4) і отримуємо рішення в аналітичному вигляді, а саме 4 вирази для визначення δ, 3 з яких не мають фізичного змісту, внаслідок від’ємного знаку перед радикалом та під радикалом . Тому єдиним раціональним рішенням диференціального рівняння (4) є :

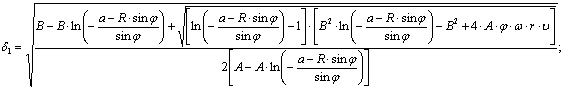(5)

За допомогою пакета MathCad 15 задавши фізичні параметри рідини, швидкість обертання диска і габаритні розміри (R = 0,1 м , а = 0,005 м , ρ = 1050 кг/м³ , ν = 5 · 10 ^{- 6}м²/c , n = 60 об/хв), отриманий масив значень товщини прикордонного шару рідини поблизу диску, що обертається, за отриманими значеннями побудована поверхня у відносних одиницях довжини (Рис. 2. а, б).

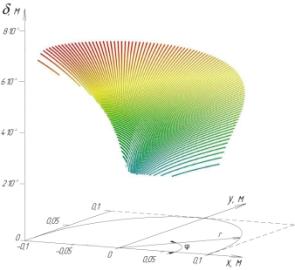
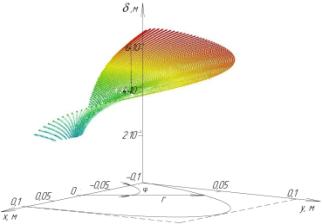
Рис. 2. Графік поверхні пограничного шару, при зануренні диска в культуральну рідину.

Було поставлено завдання визначення величини та розподілу напруження зсуву по поверхні дискової насадки внаслідок її обертання, в зв’язку з тим, що дані напруження досягаючи певних значень, можуть пошкоджувати живі клітини, що негативно впливатиме на готовий концентрат. З фізичної точки зору в процесі обертання дискової насадки відбувається захоплення розчину, що концентрується, внаслідок чого спостерігається ковзання одного шару рідини відносно іншого. Величина зміщення залежить від динамічної в’язкості розчину μ та від швидкості зсуву (рис. 3).

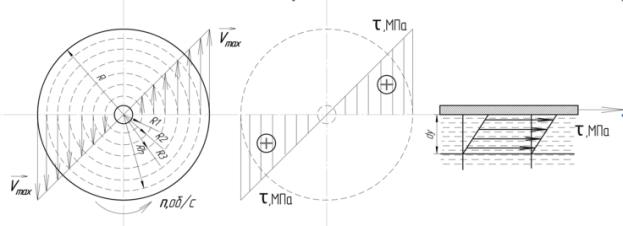
Рис.3. Розрахункова схема для визначення напружень зсуву по поверхні дискової насадки.

Напруження зсуву по поверхні дискової насадки :

(6)

Швидкість зсуву вздовж поверхні дискової насадки :

(7)

де - товщина пограничного шару рідини по поверхні дискової насадки (відповідно до математичної моделі лежить в межах від до ).

Колова швидкість по поверхні дискової насадки :

. (8)

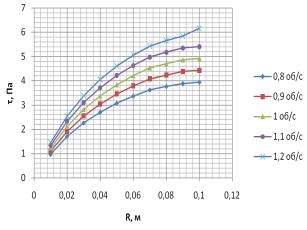
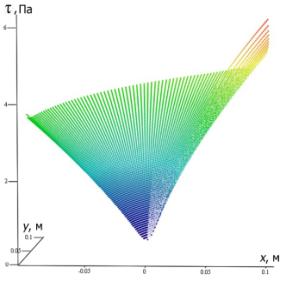
а б

Рис. 4. а - Зміна величини напружень зсувупо радіусу дискової насадки, в залежності від числа обертів; б – 3D поверхня напружень зсуву по поверхні дискової насадки.

Оскільки швидкість зсуву змінюється по радіусу дискової насадки, було розраховано поле напружень зсуву від різних значень чисел обертів(рис. 4. а, б). Відповідно літературних даних критичним значенням напружень зсуву від дії перемішуючих пристроїв є 10-50 Па, отже оптимальним діапазоном чисел обертів можна вважати значення до 1,2 об/с.

ВИСНОВКИ

Запропонована математична модель гідродинаміки та методика розрахунку напружень зсуву, дозволяє визначати оптимальні робочі параметри промислового роторно-дискового плівкового випарного апарату і може бути використана при проектуванні типового обладнання інших типорозмірів і продуктивності.

Литература:

1. Шлихтинг Г., Теория пограничного слоя [Текст] / Г. Шлихтинг // М.: Наука – 1969. – 728.
2. Лаврентьев М.А. Проблемы гидромеханики и их математические модели [Текст] / М. А. Лаврентьев, Б. В. Шабой // М.: Наука – 1973. – 225.