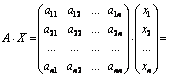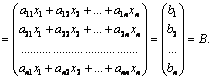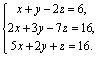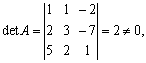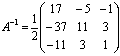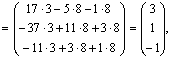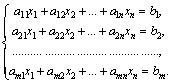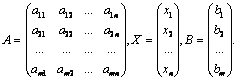Товма
Н.А.
Доктор
(PhD), доцент
Матричные методы
применяемые в учебном процессе
|
Введем
матрицу системы
и
матрицы Представим систему (1.10) в виде матричного
уравнения АХ=В. Это легко проверить, перемножив матрицы А и Х. Действительно,
Решим теперь матричное уравнение А·Х=В. Умножим обе
части уравнения на матрицу А-1 слева. Тогда А-1·А·Х = А-1·В,
а так как А-1·А=Е,
то имеем Е·Х=А-1·В и, наконец, Х = А-1·В (1.) Пример
1. Матричным методом решить систему
уравнений
Решение. Вычислим определитель матрицы А.
то
есть матрица А невырожденная. Построим обратную матрицу А-1.
Вычислим алгебраические дополнения элементов матрицы А:
Следовательно,
Находим
теперь решение системы по формуле (2).
|
|
|
|
Пусть
задана система m линейных уравнений с n неизвестными общего вида
или,
в матричной форме, А·Х = В, где
Если
В=0, то система называется однородной, в противном случае она называется
неоднородной. Решением
системы называется совокупность значений неизвестных х1=α1,
х2=α2, …, хn=αn, при
подстановке которых все уравнения системы обращаются в равенства. Система,
имеющая хоть одно решение, называется совместной. Система, не имеющая ни одного решения, называется
несовместной. Система,
имеющая единственное решение, называется определенной. Система,
имеющая более одного решения, называется неопределенной. Назовем
расширенной матрицей системы матрицу, полученную из А добавлением к ней
столбца свободных членов системы:
Так
как каждый минор матрицы А является и минором матрицы |
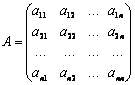

 .
Пусть
.
Пусть