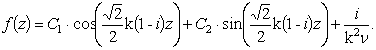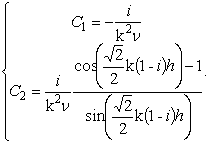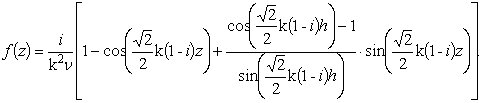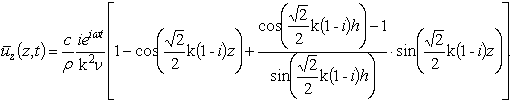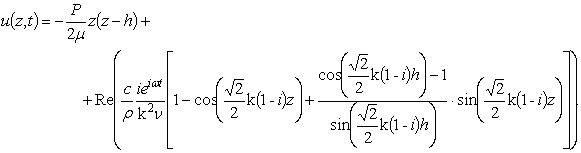Математика/5. Математическое моделирование

К.т.н. Бойчук И.П., к.т.н. Карташев А.С.

Белгородский государственный технологический университет
им. В.Г. Шухова, Россия,
Национальный аэрокосмический университет им. Н.Е. Жуковского «ХАИ», Харьков, Украина

Периодическое течение между пластинами в слое газовой смазки

Стационарное движение среды в слое газовой смазки представлено в [1]. Развитие техники привело к необходимости рассмотрения нестационарных процессов в газовой смазке.

Рассмотрим колебания жидкости между двумя параллельными пластинами, вызванное наложением на стационарное течение периодического изменения перепада давления. Направим ось вдоль пластин, а ось – перпендикулярно вверх. Рассматриваемое течение не зависит от оси , поэтому система уравнений Навье - Стокса сведется к уравнению [2]

с граничным условием на пластинах при и .

Пусть давление изменяется по закону , где является периодической функцией. Поскольку можно разложить в ряд Фурье, представим эту функцию в виде , где – константа, в общем случае комплексная [3]. Причем физический смысл имеет только вещественная часть . Тогда

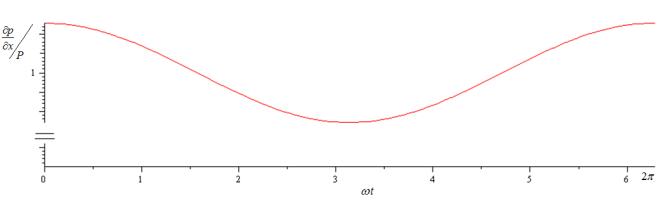
Рис. 1 Градиент давления

Далее, для скорости можем записать

(1)

где первый член описывает распределение скорости при стационарном течении [4], а определяется из уравнения

(2)

Примем для скорости следующее выражение

(3)

Подставив это выражение в (2), получим для распределения амплитуды следующее дифференциальное уравнение

где . Решением этого уравнения есть

Константы найдутся из условия равенства нулю скорости на пластинах: и , откуда , и

(4)

С учетом констант (4) решение представится в виде

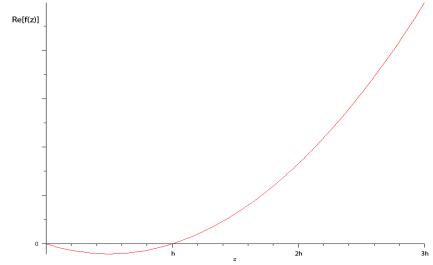
Рис. 2 График функции

Скорость будет равна

(5)

Подставляя (5) в (1), получим

(6)

Выражение (6) описывает распределение скоростей между пластинами при условии наложения периодического изменения градиента скорости на стационарное течение.

Литература:

1. Константинеску В.Н. Газовая смазка. – М.: Машиностроение, 1968. –
709 с.

2. Шлихтинг Г. Теория пограничного слоя. – М.: Наука. Гл.ред. физ.-мат. лит., 1974. – 712 с.

3. Drazin P. G., Riley N. The Navier-Stokes Equations: A Classification of Flows and Exact Solutions (London Mathematical Society Lecture Note Series), Cambridge University Press, 2006. –196 p.

4. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: учебное пособие. Т. VI. Гидродинамика. – М.: Наука. Гл.ред. физ.-мат. лит., 1986. – 736 с.