Математика/ 5. Математическое моделирование

Булгаков О.М. Пакляченко М.Ю.

Воронежский институт МВД России

Оценка сходимости итерационного алгоритма решения систем линейных алгебраических уравнений

Для определения эффективности любого вычислительного процесса, в том числе, итерационного, одним из важнейших критериев выступает сходимость численного метода, которая означает близость получаемого численного решения задачи ( значение искомой величины на ом шаге) к истинному решению (). Соответственно, факт сходимости итерационного алгоритма заключается в том, что при некотором итерационном процессе, генерирующем последовательность , имеется ее предел в .

При исследовании итерационного метода обнаружение и подтверждение факта его сходимости зачастую является недостаточным, необходимо определить меру, характеризующую процесс приближения найденных значений к . Очевидной оценкой выступает скорость сходимости. Отметим здесь, что отождествлять термины сходимость метода, решения, процесса, последовательности не совсем корректно, однако, в процессе изучения научных трудов, установлена частая синонимичность этих понятий.

Относительно вопросов измерения скорости сходимости существуют различные точки зрения. Например, в [1] утверждается, что о скорости сходимости метода можно судить по минимальному числу итераций, при котором выполнено достижение заданной точности. В учебнике [2] говорится об увеличении количества десятичных знаков точности от итерации к итерации как о характеристике скорости сходимости решения.

В работе [3] приводятся различные типы сходимости, при которых скорость определяется значением коэффициентов или степени в уравнениях:

	(1)
	(2)

Говорят, что сходимость последовательности называется линейной (итерационный процесс - линейно сходящимся), если существует постоянная (неравенство (2) при ); сверхлинейной, если существует такая положительная последовательность , что (неравенство (1)); последовательность сходится по меньшей мере с ым порядком, если найдутся такие и , что выполняется неравенство (2). При процесс квадратично сходящийся, - кубическая скорость сходимости.

Если константы не удается найти, но установлено неравенство (1) c , то в этом случае говорят об асимптотически линейной сходимости, аналогично определяют асимптотически ый порядок.

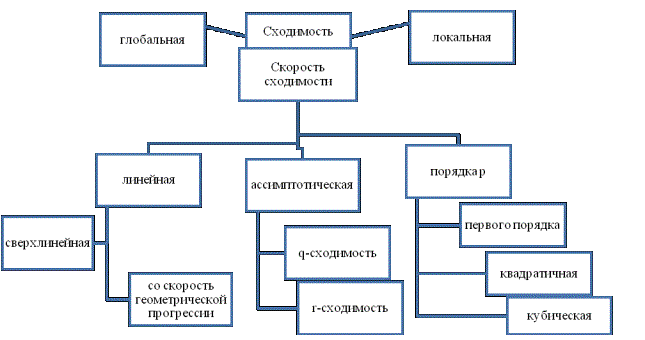
Рис.1. Классификация сходимости итерационного процесса

Большой интерес представляет сходимость множества возможных итерационных последовательностей, генерируемых итерационным методом при варьировании начального приближения () в границах некоторой области. Итерационные методы, дающие в пределе решение данной задачи при любом начальном приближении называются глобально сходящимися и локально сходящимися, в случае, если взято из достаточно малой окрестности .

Обобщение всех описанных вариантов характеристики скорости сходимости представлено на схеме (рис. 1):

Рассмотрим алгоритм решения СЛАУ, приведенный в [4] (рис. 2).

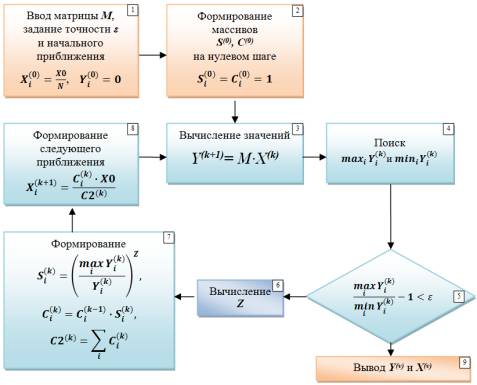
Рис. 2. Блок-схема итерационного алгоритма решения СЛАУ

Необходимо обратить внимание на ряд принципиальных моментов:

- работа алгоритма, основанного на методе простых итераций, направлена на поиск сразу двух величин: и (блок 3), при известной матрице (блок 1);

- условие остановки происходит путем сравнения значений по (блок 5);

- в формировании нового приближения участвуют служебные массивы и коэффициент , которые так же предназначены для обеспечения сходимости и устойчивости решения (блоки 7 и 8)

- имеется возможность сокращения числа итераций, путем ввода одного из служебных массивов в степень (блоки 6 и 7).

Проведем анализ скорости сходимости данного алгоритма без процедуры ускорения решения () на основе численных значений и , (, где номер итерации, на которой достигнута требуемая точность ) для различных матриц .

Для симметричной квадратной матрицы размера со следующими значениями коэффициентов, обладающих слабой неоднородностью ( и ):

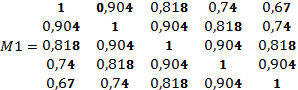
получены две последовательности и , численное значение элементов которых отображено на графиках рис 3:

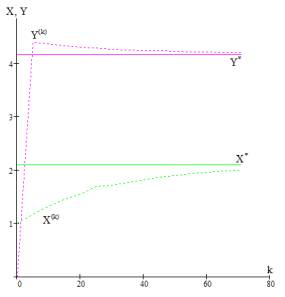
Рис. 3. Сходимость последовательностей и , найденных по итерационному алгоритму решения СЛАУ, к точному решению

Как видно по пунктирным линиям графика числовые последовательности обеих искомых величин монотонно сходятся к точному решению, при достигнута требуемая точность.

Для симметричной квадратной матрицы размера с значениями коэффициентов, обладающими высокой неоднородностью ( и ) сходимость решений, найденных по данному алгоритму имеет аналогичное рис 3 графическое представление. Однако требуемая точность для решения СЛАУ, заданной матрицей достигнута значительно раньше: на 7-ой итерации ().

Дальнейшее исследование сходимости алгоритма решения СЛАУ для симметричных квадратных матриц, в составе которых диагональные элементы равны единице, а значения других элементов в каждой строке монотонно убывают по мере отдаленности от диагонального элемента, показало, что вне зависимости от размера матрицы и неоднородности в значениях ее элементов, характер сходимости (форма пунктирной линии) не менялся, а величина для матриц со слабой неоднородностью была значительно больше, чем для матриц с высокой неоднородностью.

Найдем значения величин и из неравенств (1) и (2) для числовых последовательностей искомых величин, полученных в результате решения матрицы . С учетом специфики работы алгоритма (нахождение и ) рассматриваются коэффициенты относительно двух последовательностей: и .

Определено, что для обеих искомых величин значения . Таким образом, можно сделать вывод, что последовательности и обладают асимптотически линейной сходимостью. Аналогично найдены значения степени (рис. 5).

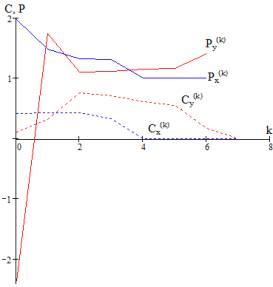
Рис. 5. Характеристики скорости сходимости итерационного алгоритма

Области допустимых значений величин и для других матриц разного размера и с коэффициентами разной степени неоднородности составили: и . Отметим, что в область допустимых значений степени не включены ее отрицательные значения, т.к величина зависит от выбора начального приближения . В алгоритме они задаются равными нулю, в случае их положительного значения, степень .

Исследование процесса нахождения решений для разных значений начального приближения ( и ) выявило, что решение сходилось к точному значению для , однако имела место и расходимость для вектора , содержащего различные значения своих компонентов. Относительно «внутреннего равенства» в наблюдалась сходимость с асимптотически линейной скоростью. В соответствии с этими наблюдениями рассматриваемый итерационный алгоритм можно классифицировать как глобально сходящийся по и локально сходящийся по .

Так как среди вычислительных операций, реализуемых данным итерационным алгоритмом решения СЛАУ, имеется процедура ускорения нахождения решения, то целесообразно определить скорость сходимости числовых последовательностей и , получаемых при введении служебного массива в степень , значение которой различны на каждом итерационном шаге(блок 7).

Для матриц коэффициентов СЛАУ и решение нашлось за 5 итераций. Графически скорость сходимости числовых последовательностей решений и представлена на рис. 6.

По графикам рис. 6 видно, что кривая значений последовательности по форме значительно отличается от кривой для , изображенной на данном рисунке и для кривой на рис. 3.

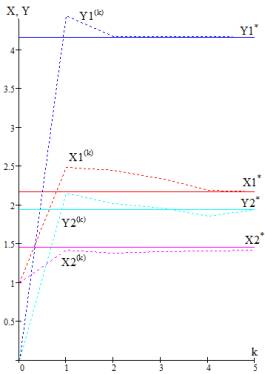
Рис. 6. Сходимость для матрицы и для матрицы , найденных по итерационному алгоритму c процедурой ускорения решения

Для значений коэффициентов и показателя степени из неравенств (1) и (2) можно отметить, что они различны для каждой задаваемой квадратной матрицы . Например, для , , , (рис. 7).

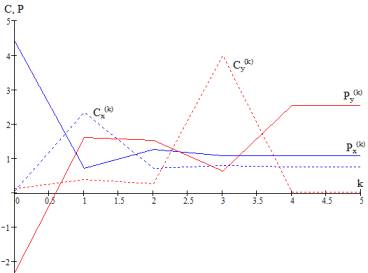
Рис. 7. Нахождение характеристик скорости сходимости итерационного алгоритма решения СЛАУ c процедурой ускорения

Непостоянство рассматриваемых величин, так же как и отсутствие стремления последовательности их значений к определенной величине объясняется влиянием степени , численные значения которой различные на каждой итерации. В связи с этим видится не совсем корректным описание скорости сходимости данного алгоритма решения СЛАУ в рамках значений коэффициентов или показателя степени .

Выводы: Основываясь на исследовании решения симметричных и не симметричных (в том числе, разряженных) квадратных матриц с диагональным преобладанием элементов (), можно классифицировать рассматриваемый итерационный способ решения СЛАУ без процедуры ускорения как алгоритм первого порядка с асимптотически линейной скоростью сходимости, глобально сходящийся по и локально сходящийся по . Однако, учитывая процедуру сокращения числа итераций, и обращая внимание на специфичность работы метода и сильную зависимость скорости решения от исходных численных данных (отраженных в матрице коэффициентов ), удобнее оценивать скорость сходимости решения конкретной задачи числом итераций, без применения общих характеристик, относящихся к порядку итерационного метода или его линейности.

Литература:

1. Самарский А. А. Введение в численные методы. Учебное пособие для вузов. 3-е изд., стер. -СПб.: Издательство «Лань», 2005. -288 с.

2. Мэтьюз Дж.Г., Финк К.Д. Численные методы. Использование Matlab. - М.: «Диалектика», 2001. - 720 с.

3. Вержбицкий В.М. Численные методы (линейная алгебра и нелинейные уравнения): Учеб. пособие для вузов. - М.: Высш. шк., 2000. - 266 с.

4. О.М Булгаков, М. Ю. Пакляченко. Способ ускорения сходимости структурно-ориентированного алго-ритма решения системы линейных алгебраических уравнений // Вестник Воронежского института МВД России. - 2014. - №2. - С. 190 -195.