МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СТАЦИОНАРНОЙ МОДЕЛИ НЕСЖИМАЕМОГО
РАСПЛАВА
С.Ш. Кажикенова, К.О. Реттих
Карагандинский государственный университет
им.Е.А.Букетова
г. Караганда, Казахстан
Расширение областей
использования металлических расплавов в качестве рабочих тел и теплоносителей в
ядерной энергетике, химии, космической технике и других отраслях
промышленности, потребности металлургического производства и новых технологий
материалов делают задачу исследования их теплофизических свойств, и в частности
вязкости, актуальной. Необходимость исследования свойств расплавов определяется
как растущими потребностями техники, так и научным значением получаемых
результатов. Всякое движение расплава можно описать системой уравнений Навье – Стокса.
В ограниченной области ![]() рассмотрим следующую
систему нелинейных стационарных
уравнений:
рассмотрим следующую
систему нелинейных стационарных
уравнений:
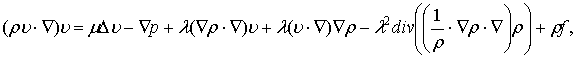 (1)
(1) ![]() ,
(2)
,
(2)
![]() ,
(3)
,
(3)
с граничными условиями:
![]() ,
, ![]() , (4)
, (4)
где ![]() вектор-функция скоростей,
вектор-функция скоростей, ![]() поле плотностей,
поле плотностей, ![]() поле давления расплава,
поле давления расплава, ![]() вектор массовых сил,
вектор массовых сил, ![]() коэффициенты диффузии
и вязкости,
коэффициенты диффузии
и вязкости,![]() достаточно гладкая граница области
достаточно гладкая граница области ![]() . Разрешимость задачи (1) – (4) была исследована в
работе [1]. Известно, что система
уравнений (1) – (3) неэволюционная и
поэтому прямое применение численных методов затруднительно. Для разрешения этой
проблемы мы будем рассматривать другую модель неоднородного расплава,
являющуюся аппроксимацией исходной модели
(1) – (4) с малым параметром
. Разрешимость задачи (1) – (4) была исследована в
работе [1]. Известно, что система
уравнений (1) – (3) неэволюционная и
поэтому прямое применение численных методов затруднительно. Для разрешения этой
проблемы мы будем рассматривать другую модель неоднородного расплава,
являющуюся аппроксимацией исходной модели
(1) – (4) с малым параметром ![]() :
:
![]()
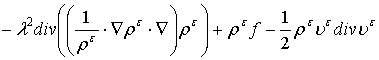 , (5)
, (5)
![]() , (6)
, (6)
![]() ,
(7)
,
(7)
с граничными условиями:
![]() ,
, ![]() , (8)
, (8)
Система уравнений (5) –
(7) является системой типа Коши-Ковалевской. Пространство 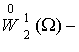 подпространство
подпространство 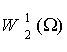 , является замыканием множества бесконечно-дифференцируемых
финитных вектор - функций [2].
, является замыканием множества бесконечно-дифференцируемых
финитных вектор - функций [2].
Определение. Сильно-обобщенным
решением задачи (5) – (8) называют совокупность функций ![]() , которые удовлетворяют следующим условиям:
, которые удовлетворяют следующим условиям:
1) ![]()
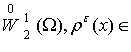
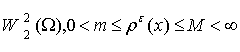 ;
;
2) ![]()
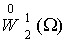 выполняется
интегральное равенство:
выполняется
интегральное равенство: 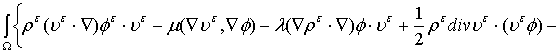
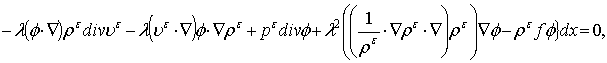 Уравнения (6),(7)
и граничные условия (8) выполняются почти всюду в
Уравнения (6),(7)
и граничные условия (8) выполняются почти всюду в ![]() по соответствующей
мере.
по соответствующей
мере.
Теорема 1 Если 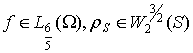 , то при достаточно малом:
, то при достаточно малом:
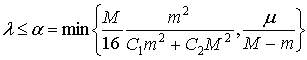 , (9)
, (9)
существует хотя бы одно сильно-обобщенное
решение задачи (5) –(8), где ![]() - константы, зависящие только от данных задачи и не зависящие
от функций
- константы, зависящие только от данных задачи и не зависящие
от функций ![]() .
.
Доказательство данной теоремы
строится из трех этапов: получение априорных оценок, использование метода
Галеркина и предельный переход. Сначала получим необходимые априорные оценки.
Умножим (6) на ![]() скалярно в
скалярно в ![]() :
:
![]() , (10)
, (10)
К правой части применим
интегрирование по частям:
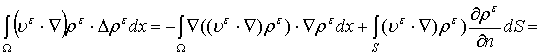
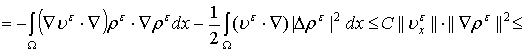
![]() .
.
По принципу максимума из
уравнения (6) получим:
![]() , (11)
, (11)
Следовательно:
![]() .
.
Предположим, что ![]() , тогда из (10) имеем:
, тогда из (10) имеем:
![]() . (12)
. (12)
Умножим уравнение (5) на функцию ![]() скалярно в
скалярно в ![]() :
: 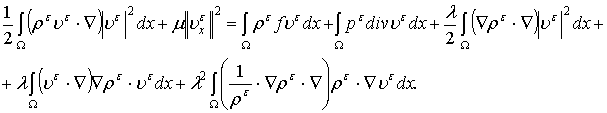 Отсюда имеем:
Отсюда имеем:
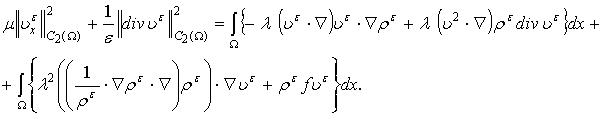 Далее,
оценивая интегральные слагаемые также как в [3, с.187], получим:
Далее,
оценивая интегральные слагаемые также как в [3, с.187], получим: 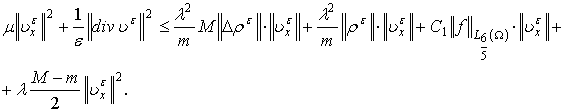
Допустим, что ![]() , то есть
, то есть ![]() . Используя неоднократно неравенство Юнга, выводим:
. Используя неоднократно неравенство Юнга, выводим:
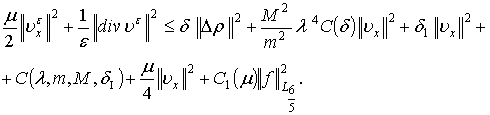
Выберем ![]()
![]() и, учитывая (3), получим
оценку:
и, учитывая (3), получим
оценку:
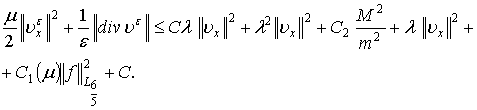
Далее допустим, что ![]() и
и 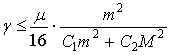 . Тогда:
. Тогда:
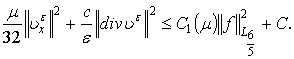
Таким образом, имеем оценку:
![]() (13)
(13)
при достаточной малости
![]() :
:
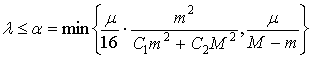 . (14)
. (14)
На основании теорем вложения [2] следует:
![]() . (15) Из неравенства (12) с учетом оценки (13)
вытекает:
. (15) Из неравенства (12) с учетом оценки (13)
вытекает:
![]() (16)
(16)
В силу (15) получим:
![]() (17)
(17)
Оценивая аналогично [3,
с.188] в негативной норме ![]() , имеем:
, имеем:
![]() (18)
(18)
Далее переходим к методу
Галеркина для построения приближенных
решений. Пусть ![]() базис в пространстве
базис в пространстве
![]() из следующей задачи:
из следующей задачи:
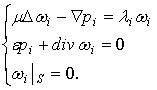 (19)
(19)
Приближенное решение ![]() представим в виде:
представим в виде:
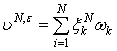 , (20)
, (20)
а плотность и давление
есть классическое решение задачи:
 (21)
(21)
![]() . (22)
. (22)
Числа ![]() находятся из
следующей системы уравнений:
находятся из
следующей системы уравнений:
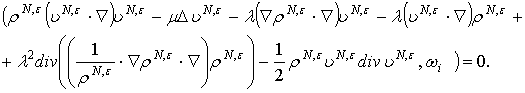
![]() .
(23)
.
(23)
Тем самым [3,с.189]
доказано существование решения задачи (20) – (23) и справедливость априорных
оценок (11), (13), (15)–(18) для приближенных решений ![]() Тогда из
последовательностей
Тогда из
последовательностей ![]() можно выделить
подпоследовательности, для которых имеем:
можно выделить
подпоследовательности, для которых имеем:
![]() * слабо в
* слабо в ![]() ,
,
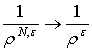 * слабо в
* слабо в ![]() ,
,
![]() слабо в
слабо в ![]() ,
,
![]() сильно в
сильно в
![]() ,
, ![]() ,
,
![]() слабо
в
слабо
в ![]() ,
,
![]() сильно в
сильно в ![]() ,
, ![]() ,
,
![]() слабо в
слабо в ![]() .
.
Далее, переходя к
пределу по выбранным последовательностям в интегральном тождестве,
соответствующим интегральному тождеству в определении и в (21) – (22)
заключаем, что предельные функции ![]() являются
сильно-обобщенным решением задачи (5) – (8).
являются
сильно-обобщенным решением задачи (5) – (8).
Теорема 1 доказана.
Теорема 2 Пусть
выполнены все условия теоремы 1, тогда сильно-обобщенное решение задачи
(5) – (8) при ![]() сходится к
сильно-обобщенному решению задачи (1) – (4).
сходится к
сильно-обобщенному решению задачи (1) – (4).
Доказательство. В силу
равномерных априорных оценок имеем:
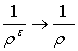 * слабо в
* слабо в ![]() ,
,
![]() * слабо в
* слабо в ![]() ,
,
![]() слабо в
слабо в ![]() ,
,
![]() сильно в
сильно в ![]() ,
, ![]() ,
,
![]() слабо в
слабо в ![]() ,
,
![]() сильно в
сильно в ![]() ,
, ![]() ,
,
![]() сильно в
сильно в
![]() .
.
Далее, переходя к
пределу при ![]() в соответствующих
тождествах, легко устанавливаем, что предельные функции
в соответствующих
тождествах, легко устанавливаем, что предельные функции ![]() есть
сильно-обобщенное решение задачи (1) – (4).
есть
сильно-обобщенное решение задачи (1) – (4).
Теорема 2 доказана.
Список литературы
1. Антонцев С. Н.,
Кажихов А. В., Монахов В. Н. Краевые задачи механики неоднородных
жидкостей. – Новосибирск: Наука, 1983,
318 с.
2. Ладыженская О. А.
Математические вопросы динамики вязкой несжимаемой жидкости. – М.: Наука, 1970,
288 с.
3. Смагулов Ш. С.,
Байтуленов Ш. Б. Корректность одной диффузионной стационарной модели
неоднородной несжимаемой жидкости. //Труды
международной конференции «Современное
состояние и перспективы развития математики в рамках программы: Казахстан в
третьем тысячелетии», 26-28 октября, Алматы, 2000, С.185-189.