Листопадова В.В.
Національний
технічний університет України «КПІ»
ОСОБЛИВОСТІ КІНЕМАТИКИ ПРОМИСЛОВИХ РОБОТІВ
Робототехніка як новий напрям науки і техніки пов'язана
зі створенням та застосуванням роботів і робототехнічних систем.
Робототехніка сформувалась як науковий напрям у другій
половині XX ст. її бурхливий розвиток
розпочався в 70-ті роки XX ст. Особливістю
робототехніки є те, що вона вивчає кінематику і динаміку сукупності твердих
тіл (найчастіше двох - п'яти).
Науковою базою робототехніки є теоретична механіка. В
робототехніці, з одного боку, використовуються основні доробки всіх розділів
теоретичної механіки, а з іншого боку, робототехніка як наука поєднує по суті
теоретичну механіку, кібернетику та комп'ютерні технології. Основою останніх,
як відомо, є операції з матрицями.
Відомі алгоритми, є найбільш загальними і охоплюють найскладніші випадки
з'єднання і взаємодії тіл. У промислових роботах з'єднання двох тіл або їх
взаємодія характеризується не за допомогою шести координат, а, як правило, за
допомогою однієї координати, тобто тіло ІІ
(рис. 1) може переміщатися відносно тіла І або за допомогою
телескопічної (призматичної) пари, яка організовує лише поступальний рух тіла II відносно тіла І і лише по одній координаті, або за
допомогою обертальної пари, яка уможливлює відносний поворот тіл лише на один
кут повороту (циліндричний шарнір).
Разом з тим у техніці розповсюджені й такі з'єднання або
взаємодії тіл, що реалізуються через два кути повороту, наприклад карданна
передача, або через усі три -гіроскоп у кардановому підвісі.
Шість ступенів вільності реалізуються при русі літальних
та плавучих об'єктів (літаків, кораблів, підводних апаратів, ракет, космічних
апаратів) у гіроскопічних приладах з так званими безконтактними підвісами
гіроскопа - електромагнітними, аеродинамічними, електростатичними - або в
приладах із пружними підвісами тощо.
Спільним для всіх цих систем є те, що взаємодіє велика
кількість тіл, які утворюють системи з багатьма (дві і більше) ступенями
вільності.
Розглянемо особливості кінематики роботів, що складаються із п твердих
тіл, які містять з'єднання, що є телескопічними чи обертальними парами.
Викладено цей матеріал за методикою проф. О. П. Бойчука.
Нехай маємо
маніпуляційний робот із п тіл або ланок. Зв'яжемо з к-ю ланкою систему
координат ![]() .
.
Координати довільної точки (або її радіус-вектор) k-ї ланки в системі
координат, зв'язаної з цією ланкою, описуються чотирикоординатним вектором
![]() , (1)
, (1)
або однорідними
координатами
![]() . (2)
. (2)
При цьому результуюча матриця переходу 4x4 дорівнює
![]() (3)
(3)
Установимо правила, за якими можна було б отримати
результуючу матрицю переходу ![]() у випадку наявності в системі
вказаних кінематичних пар – телескопічної чи обертальної.
у випадку наявності в системі
вказаних кінематичних пар – телескопічної чи обертальної.
Телескопічна пара – відносний рух k-ї ланки прямолінійний,
поступальний.
Вісь ![]() системи координат
системи координат ![]() , зв'язаної з
k-ю ланкою, направимо по
лінії переміщення (або паралельно йому) так, щоб вона проходила через точку
, зв'язаної з
k-ю ланкою, направимо по
лінії переміщення (або паралельно йому) так, щоб вона проходила через точку ![]() , тоді відстань
, тоді відстань ![]() приймемо за координату (рис. 2).
приймемо за координату (рис. 2).
Матриця напрямних косинусів між вказаними системами
координат має вигляд:
![]()
![]()
![]()
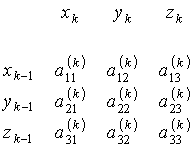 (4)
(4)
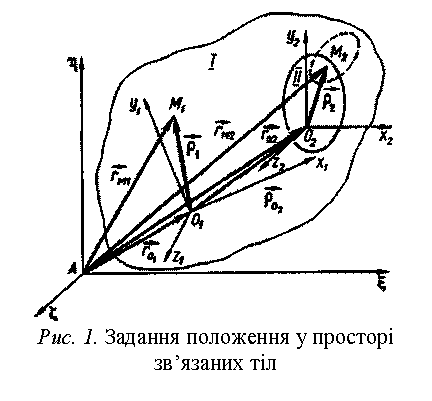
Координати довільної точки М k-і ланки в системі координат ![]() (рис. 2)
визначаються виразом
(рис. 2)
визначаються виразом
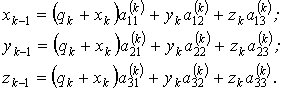 (5)
(5)
Чотиривимірна матриця переходу ![]() від системи координат
від системи координат![]() , зв'язаної з k-ю ланкою, до системи координат
, зв'язаної з k-ю ланкою, до системи координат ![]() , зв'язаної
з
, зв'язаної
з ![]() -ю ланкою, що характеризує телескопічну (призматичну) в'язь,
буде
-ю ланкою, що характеризує телескопічну (призматичну) в'язь,
буде
![]()
![]()
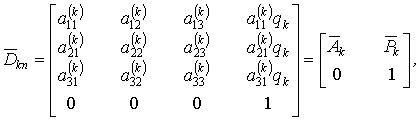 (6)
(6)
де індекс "п" матриці
переходу ![]() відображає поступальний рух;
відображає поступальний рух; ![]() –– матриця напрямних косинусів;
–– матриця напрямних косинусів; ![]() – вектор-стовпець, що характеризує положення точки
– вектор-стовпець, що характеризує положення точки
![]() в системі координат
в системі координат ![]() .
.
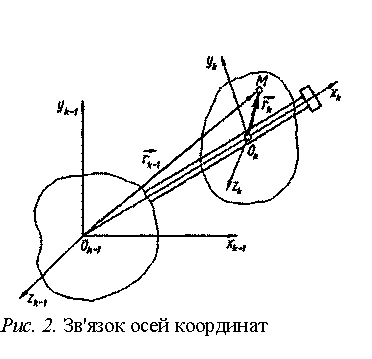
Обертальна пара. У цьому випадку систему координат
![]() обирають так, щоб одна з осей координат, наприклад
обирають так, щоб одна з осей координат, наприклад
![]() , збігалася б із віссю обертання, а положення точки
, збігалася б із віссю обертання, а положення точки ![]() на осі
на осі ![]() вибирають довільно (рис. 3).
вибирають довільно (рис. 3).
За узагальнену координату приймемо кут ![]() повороту ланки відносно початкового положення
повороту ланки відносно початкового положення
![]() системи координат
системи координат ![]() . Якщо початкове положення системи координат
. Якщо початкове положення системи координат ![]() в системі
в системі ![]() характеризується матрицею напрямних косинусів
характеризується матрицею напрямних косинусів
![]()
![]()
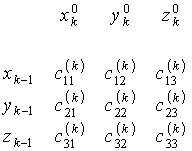 , (7)
, (7)
то координати довільної точки М k-ї ланки в системі координат ![]() будуть наступними:
будуть наступними:
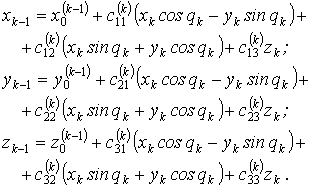 (8)
(8)
Тоді чотиривимірна матриця переходу (обертання) набере вигляду:
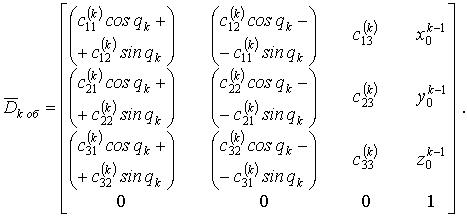 (9)
(9)
Тут індекс "об" означає обертання; ![]() ,
, ![]() ,
, ![]() – координати точки
– координати точки ![]() в системі координат
в системі координат ![]() (рис. 4).
(рис. 4).
Тепер формули (5) та (8) можна записати так:
для телескопічної пари
![]() , (10)
, (10)
для обертальної пари
![]() , (11)
, (11)
Координати довільної точки М k-ї ланки в системі
координат, зв'язаній з основою механізму, матимуть вигляд
![]()
![]()
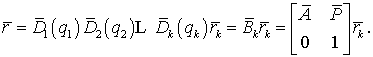 (12)
(12)
Визначимо тепер кінематичні характеристики маніпулятора і довільної точки М
k-ї ланки.
Для абсолютної швидкості точки М отримаємо
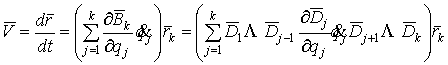 (13)
(13)
і відповідно для прискорення
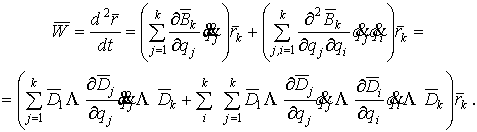 (14)
(14)