В.И. Алехин, Л.А. Рутковский, В.А. Созаев, М.А. Ковалева

ФГБОУ ВПО Северо-Кавказский горно-металлургический институт (ГТУ)

Сингулярно-возмущенная диффузия

Пограничные слои, как правило, это множества, которые представляют собой окрестности какой-либо точки, линии или вообще многообразия меньшей размерности. Данная окрестность имеет ширину порядка ε^y, где γ является малым параметром. Данное множество является частью границы области. Функции, описывающие асимптотику решения в пределах пограничного слоя, называются функциями пограничного слоя или, сокращенно, погранслойными функциями.

В одномерном случае возникает следующая краевая задача для уравнения диффузии

, , , (1)

где U(x) - концентрация; ε - малый параметр.

Краевая задача имеет следующее единственное решение:

(2)

В (2) погранслойньми функциями являются ехр(-xε^-1) и exp((1-x)ε^-1). Эти функции существенно отличны от нуля лишь в окрестности точек «ноль» и «единица» соответственно.

Рассмотрим более общую краевую задачу.

, (3)

. (4)

Решение (3), (4) представим в виде суммы асимптотических рядов:

, , (5)

Здесь , .

Предположим, что функции и_k, w_k экспоненциально убывают на бесконечности. Учитывая, что для значений х, которые лежат внутри [0,l], коэффициенты рядов V, W экспоненциально малы при ε→0, следовательно, U удовлетворяет уравнению (3), а V и W однородным уравнениям . Подставим ряд и в уравнение (3). Приравнивая нулю, коэффициенты при одинаковых степенях, получим рекуррентную систему уравнений:

, (6)

, при k≥1.

Таким образом, система (6) определяет все . Уравнение, определяющее ряд V имеет вид:

. q_o>0. Разложим q(x) в степенной рад.

Подставим V в уравнение, в результате получим рекуррентную систему:

, , k≥1. (7)

Учитывая краевое условие в (6), получим

, , k≥0. (8)

Задачи (7), (8) имеют единственные решения. Данные решения экспоненциально стремятся к нулю при ξ→0. Функции w_k(η) определяются аналогично. Таким образом, ряды V и W не оказывают большого влияния на решение вдали от границы. Асимптотика решения определяется рядом и. Данный ряд называется внешним асимптотическим разложением. Ряды V и W называются внутренними разложениями.

Рассмотрим краевую задачу для обыкновенного дифференциального уравнения

, , (9)

, (10)

где D - ограниченная область, , , .

Будем полагать q(x)>, при x>0; q(0)=0, . Теперь лишь при х>0, при x=0 все u_k имеют особенности , . Чтобы правильно описать асимптотику решения u(x,ε) в окрестности точки х=0 проведем растяжение независимой переменной: .

Тогда из уравнения(9) получим

, (11)

Здесь обозначено . Учитывая, что q(x)~x при х→0, то полагая 3-2α= α → α =1. Таким образом, вблизи начала координат получаем и(х,ε) в виде внутреннего разложения

, (12)

где , разлагая в ряд Тейлора q(x) и f(x) получим

,

После подстановки ряда (12) в (11) получаем рекуррентную систему уравнений.

Здесь и_к(0)=0, к≥-1 - граничные условия.

, , k≥0, (13)

Для того чтобы установить влияние пограничных слоев, необходимо решить уравнение диффузии для каждой из фаз. Это уравнение в одном случаи будет иметь вид [3], [4]:

, ε→0. (14)

где с – концентрация , D - коэффициент диффузии.

Учитывая , преобразуем уравнение (14):

, , , , , отсюда следует . Подставляя в уравнение (14) в результате получим:

, (15)

Из (15) получим

, (16)

А, В - постоянные

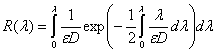, (17)

, (18)

где (-k₁≤x≤k₂) при фиксированном моменте времени равенство (18) определяет уравнение кривой распределения концентрации в жидкой фазе: 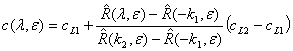, (19)

где (l₁≤l≤l₂)

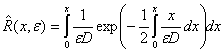, (20)

Если же коэффициент взаимодиффузии в жидкой фазе (D_L) нe зависит от концентрации, равенство (19) будет иметь следующий вид:

, (21)

(-u₁≤u≤u₂), , , , .

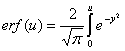где - erf(u) - интеграл Гаусса.

Продифференцируем (19), в результате получим

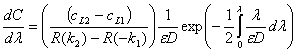, (22)

Если записать равенство (22) для граничных плоскостей λ=-k₁, λ=-k₂, тогда можно получить выражение для приграничных сингулярно-возмущенных потоков:

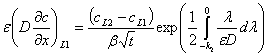, (23)

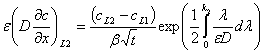, (24)

где .

Таким образом, решая уравнения (23), (24) можно изучить картину приграничных сингулярно-возмущенных потоков и их влияние на физико-химические свойства.

Учитывая, что уравнения (23), (24) являются сингулярно-возмущенными, для решения данных уравнений необходим особый подход (их регуляризация - метод обработки формализованной информации).

Результаты работы получены при поддержки проекта № 265 г/б «Развитие математических методов оптимального управления на множестве взаимосвязанных траекторий непрерывных технологических процессов», выполняемого в рамках государственного задания № 2014/207.

Список литературы:

1. М. И. Вишик, Л. А. Люстерник Регулярное вырождение и пограничный слой для линейных дифференциальных уравнений с малым параметром // Успехи мат. Наук, 12(5), 1957. - С. 3-122.

2. А. Б. Васильев, Б. Ф. Бугузов Асимптотические разложения решений сингулярно-возмущенных уравнений, М.: Наука, 1973. - С. 272.