Математика / 4. Прикладная математика

Аipanov Azamat Sh.

Süleyman Demirel University, Faculty of Economics,

Almaty, Kazakhstan

GLOBAL ASYMPTOTIC STABILITY OF OSCILLATORY-ROTARY MOTION OF A MATHEMATICAL PENDULUM

1. Introduction. The problem covered is a stability of the mathematical pendulum moving under the force of gravity, viscous friction and external force with constant moment. It is assumed that initial deviation and velocity of the pendulum may be very large, so that it is capable of exhibiting not only oscillatory, but also rotational motion. When the damping coefficient is sufficiently large the pendulum's motion becomes stable due to the dissipation of energy by the friction force. The pendulum eventually comes to a damped oscillations mode and converges to the equilibrium point. When is small there is a possibility that the pendulum will start to rotate without stopping if the external force moment acting on it prevails. Thus there is a threshold value such that when the damping coefficient , the motion of the pendulum tends to its equilibrium position with any initial conditions.

Several attempts to determine the value of made by F. Tricomi, L. Amerio, G. Seifert, W. Hayes, C. Böhm and other scientists in 30th – 50th years of the XX century were not successful. Only lower and upper estimates in the forms of and were found. It was not until 1954 when Japanese mathematician M. Urabe from the University of Hiroshima proposed a numerical algorithm [1, 2] for calculating . However, it turned out in some cases that the algorithm doesn't converge. As for the analytical formula for finding , the problem has not been solved yet.

The modification of Urabe's method proposed by the author [3] has an increased rate of convergence. The results obtained here can be used for the analysis of stability of systems with angular coordinates (phase systems) where oscillation and rotation processes take place. These are, for example, rotor systems in mechanics, synchronous generators in electric power industry, phase-locked loop (PLL) systems in radio technology and others.

2. The problem statement. The mathematical pendulum represents a rod of length , with a mass on its end. There is the force of gravity and an external force with constant moment acting on the pendulum. It moves in a viscous ambient where the force of friction is equal and is directed opposite to the velocity vector ( is a friction coefficient which depends on ambient viscosity, is a velocity of the pendulum). It is assumed that the inequality is satisfied.

The motion of the mathematical pendulum considered here is described by the system of differential equations [4]

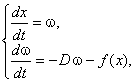(1)

which can be reduced to the form

(2)

where ; is an angle of the pendulum's deviation from the vertical; ; is an angular velocity; a parameter is a damping coefficient; is a -periodic function; .

On the set the function turns to zero at two points: at and at . We designate and point out that the following relationships are true:

, ; , ; , .

The stationary set of the system (1) on the plane consists of the stable equilibrium points (, ) and the unstable equilibrium points (, ), where .

Let's denote the solution of the system (1) with the initial conditions , as the functions , , where .

D e f i n i t i o n . The system (1) is called globally asymptotically stable, if its solution (, ) for any initial conditions , goes with to some (stable or unstable) equilibrium state from the set .

We consider on the plane two special phase trajectories: which starts from the unstable equilibrium point (, ) and which tends to the unstable equilibrium point (, ). The images of the phase trajectories , corresponding to the cases a) , b)  and c)  are presented on the Figure 1.

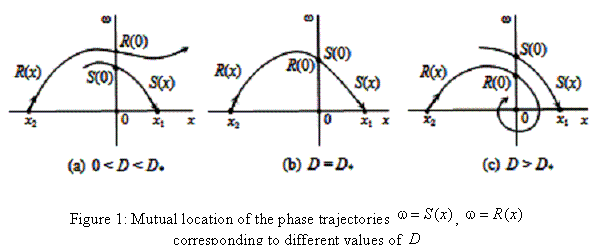
T h e o r e m   1 . (E.A. Barbashin and V.A. Tabuyeva [4, p. 70]). There exists a unique value of such that the following relationships hold true (Figure 1):

a) when , (3)

b) when , (4)

c) when . (5)

Thereby, as follows from Theorem 1, the two phase trajectories and merge together: , , when (Figure 1 (b)). The criterion of the global asymptotic stability of the system (1) has a form of an inequality , setting the problem of determining the value of .

3. Modification of the Urabe's algorithm. The Urabe's original algorithm [1, 2] is based on assumption of analyticity of the function on the segment . But as the Figure 1 (c) suggests, when the phase trajectory cannot be represented as power series on the segment . This is the main disadvantage of the Urabe's algorithm. The modification of this method is rather based on Theorem 1 by E.A. Barbashin and V.A. Tabuyeva and the expansions of the functions , into Taylor series on the segments , respectively.

Step 1. Expanding the function on the segment into the Taylor power series we get

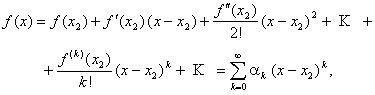(6)

where . Repeat the same procedure with on the segment

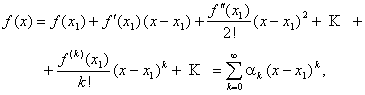(7)

where . Whereas and is a -periodic function the following equalities hold true: , , moreover , .

Step 2. The sought-for value of lies on the segment , where can be taken as any of the lower estimations and can be taken as any of the upper estimations . Let us take the first approximation equal to .

Step 3. We seek the function which satisfies the equation

(8)

on the segment in the form of power series

(9)

where ,

Step 4. Plugging the series (6) and (9) into the formula (8) we get the equation

which can be written as . Equating the coefficients , to zero we get the system of equations

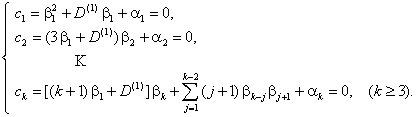
From this we find the values of :

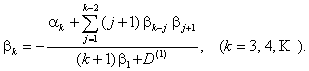
Here is a positive root of the quadratic equation because , .

Step 5. Plugging the found coefficients into the formula (9) we calculate the value .

Step 6. We are searching for the function that satisfies the equation

(10)

on the segment in the form of power series

(11)

where ,

Step 7. Plugging the series (7) and (11) into the formula (10) we get the equation

which can be reduced to . Equating the coefficients , to zero, we get the system of equations

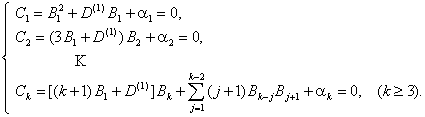
From this we find the values of :

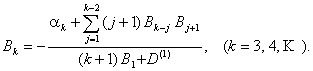
Here is a negative root of the quadratic equation since , .

Step 8. Plugging the found coefficients into the formula (11) we calculate the value of .

Step 9 (dichotomy method). Let's consider the following three cases:

9a) If , then from (3) follows that $, i.e. the value of lies in the segment . We take the next approximation equal to .

9b) If , then from (4) follows that , i.e. we found – the sought-for value of the damping coefficient. The algorithm stops.

9c) If , then from (5) follows that , i.e. the value of lies in the segment . We take the next approximation equal to .

During the computer implementation of this algorithm the fulfillment of the condition serves as a criterion of stoppage of the algorithm on the step 9b, where is a sufficiently small number which specifies the accuracy of calculations. If this inequality doesn't hold true, on the step 9a or 9c we determine the segment which contains and the length of this segment is going to be half the length of the initial segment .

Next we repeat the steps 3-9 taking the value of instead of ; determine the segment which contains and select the middle point of this segment as a next approximation and so forth. Thus, on the th iteration the length of is going to be times smaller than the length of , which means that it is possible to reach very high accuracy in a reasonable amount of iterations. Furthermore, one should consider as many summands in the expansions (6), (7), (9) and (11) as needed to achieve the given accuracy of calculations.

4. Numerical example. Let us look at the numerical example illustrating the efficiency of the proposed modification of the Urabe's algorithm. We consider the equations of the mathematical pendulum motion (1) with following values of parameters

, , . (12)

Using the formulas for lower and upper estimates of we can determine the interval in which lies. Notably, there are following lower estimations [4] in the form of inequality :

(a) F. Tricomi estimate:

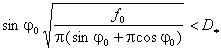; (13)

(b) W. Hayes estimate:

; (14)

(c) C. Böhm estimate:

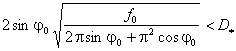. (15)

There are also the upper estimates [4] in the form of :

(d) G. Seifert estimate:

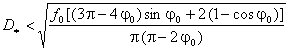; (16)

(e) F. Tricomi estimate:

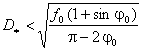; (17)

(f) L. Amerio estimate:

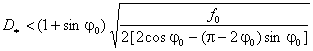. (18)

For the example considered here the following estimates were gained from the formulas (13)-(18):

(a) ; (b) ; (c) ;

(d) ; (e) ; (f) .

Thus, we have the estimates for the value of . In the examined example , so the conditions are also satisfied. Meanwhile it is impossible to say anything about the mutual position of and (what of the next inequalities holds true: or ?). So we are not able to say whether the system is stable or unstable based on the estimates (13)-(18).

Computer calculations using the modified algorithm of M. Urabe showed that . From this we can see that the criterion is satisfied, which means that the system (1) with the given values of parameters (12) is globally asymptotically stable.

The calculations based on the original algorithm carried out for the different values , , , where is the number of terms in the Taylor series expansion, don't converge. On the other hand, the iteration process in the modified algorithm rapidly converges to the value , the condition , where , which signifies the end of the process, is fulfilled on the 24th iteration for .

5. Conclusion. The paper contains the results related to the stability analysis of the mathematical pendulum: the global asymptotic stability of the system under the condition , the theorem by E.A. Barbashin and V.A. Tabuyeva in existence and uniqueness of the threshold value , the upper and lower estimates of by F. Tricomi, L. Amerio, G. Seifert, W. Hayes, C. Böhm, and the modification of the Urabe's method for numerical calculation . The Urabe's original algorithm has a following drawback. When the function has a positive value at the point , while it is undefined at the point when . That is why the modified algorithm uses the expansion of the function on the segment and the expansion of the function on the segment so that there is no need to calculate . The fact that the functions are expanded into Taylor series on the segments of smaller length also leads to the increase in accuracy of the algorithm.

The values of on the segment and on the segment (as the solutions of the differential equations (8) and (11) respectively) can be also calculated numerically using Runge – Kutta method.

References:

1. M. Urabe. Infinitesimal deformation of the periodic solution of the second kind and its application to the equation of a pendulum // J. Sci. Hiroshima Univ., Ser. A, Vol. 18, 1954. – P. 183-219.

2. M. Urabe. The least upper bound of a damping coefficient ensuring the existence of a periodic motion of a pendulum under constant torque // J. Sci. Hiroshima Univ., Ser. A, Vol. 18, 1955. – P. 379-389.

3. A.Sh. Aipanov. Modification of the Urabe's method // Theses of Int. Sci. Students Conf. "VII Kolmogorov Readings", Sect. Math., Moscow, 2007. – P. 13-14 (in Russian).

4. E.A. Barbashin, V.A. Tabuyeva. Dynamic systems with cylindrical phase space. – Moscow: Nauka, 1969 (in Russian).