The honored science and education member of the RANS, corresponding-member of the IAS of HS, Dr.S. (eng.). Professor, Pil E.A. Russia, Saint-Petersburg, Saint-Petersburg State Marine Technical University

Variants of economic shell expansion and retraction

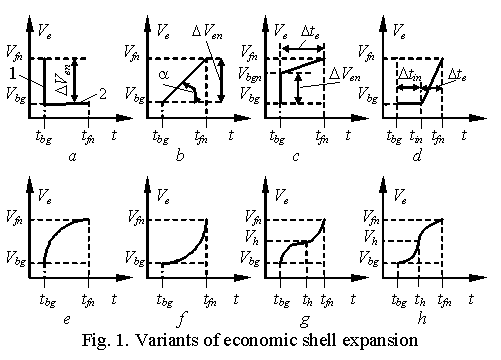
The next diagram in figure 1b shows a linear dependence where an economic shell expands rectilinearly at angle a to the horizontal axis. Angle a is situated within the following limits: 0 £ a £ 90°. This variant is desirable while an economic shell expands (retracts), as knowing the values of angle a and time Dt_e we can easily calculate both the final and intermediate volumes of the economic shell using the equation V_e = t + с.

Fig. 1с and 1d show variants of more complex development of economic shell expansion that are a group of two lines. So, Fig. 1с depicts a case where after influence of internal forces an economic shell reacted to it instantly and expanded by the value DV_en whereupon its volume changes according to the linear law.

Figures 1d and 6e show slow reaction of an economic shell after internal forces affect it. Slow response of an economic shell is characterized by the time Dt_in during which the volume of the economic shell does not change despite external (internal) forces affecting it (1)

Dt_in = t_in - t_bg, (1)

where: t_in is the end time of slow response of an economic shell.

In the case in question the bigger the value Dt_in the more intensely the volume of an economic shell will change in future.

Slow response of an economic shell after it is affected by forces shows that the market (companies) evaluates the situation change and solves the issue of how to react to it.

Thus, here we can draw the following description for slow response of an economic shell.

Slow response of an economic shell is understood as its state where after forces P_V affect it its volume V_e does not change during time Dt_in due to the market (companies) comprehending possible outcomes of these forces’ influence.

The next class of change of economic shell volume is presented in Fig. 1e, 1f, 1g, and 1h in the form of curves which can be described by a general polynomial equation (2)

So, Fig. 1e shows a variant where after internal forces affect an economic shell its volume starts to increase quickly, and then it comes smoothly to its top value. Figure 1f shows a similar dependence but at the beginning after internal forces affect an economic shell its volume changes slowly due to slow response of the system, and then changes are ascending.

Fig. 1g and 1h show almost identical complex dependences of volume change of an economic shell. These diagrams have an inflexion point with coordinates V_h and t_h where one type of mathematical dependence of volume change of an economic shell changes to another.

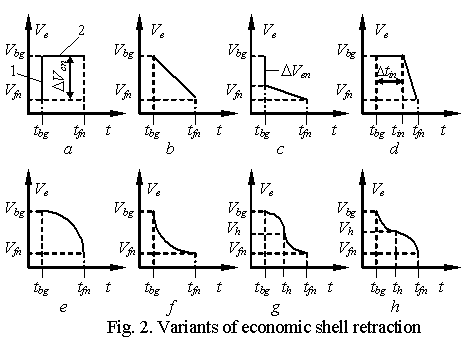
Fig. 2 shows possible variants of economic shells retraction after being affected by external forces drawn similarly to Fig. 1, and here similar conclusions are acceptable.