Стохастические модели управления запасами при удовлетворении спроса с постоянной интенсивностью

Казангапова Б.А., Чокин Н.С.

Функционирование предприятий и организаций, так или иначе, связаны с задачами управления запасами, что говорит о необходимости научного подхода к управлению ими. Для научного управления запасами необходимо правильно представлять себе роль и значение запасов, факторы и их образования, мотивы их создания.

Задача управления запасами возникает, когда необходимо создать запас материальных ресурсов или предметов потребления с целью удовлетворения спроса на заданном интервале времени (конечном или бесконечном). Для обеспечения непрерывного и эффективного функционирования практически любой организации необходимо создание запасов. В любой задаче управления запасами требуется определять количество заказываемой продукции и сроки размещения заказа. Спрос можно удовлетворить путём однократного создания запаса на весь рассматриваемый период времени или посредством создания запаса для каждой единицы времени этого периода. Эти два случая соответствуют избыточному запасу (по отношению к единице времени) и недостаточному запасу (по отношению к полному периоду времени) [1].

Стохастические модели управления запасами возникают в тех случаях, когда спрос является случайным. Этот факт существенным образом сказывается на характере соответствующих моделей и значительно усложняет их анализ.

Мы рассматривали стохастическую модель управления запасами, когда спрос случайным образом оказывается равным r с вероятностью p(r) и запасы расходовались сразу в количестве r.

Рассмотрим случай, когда (при запасе s) спрос r, появляющийся с вероятностью p(r), расходуется не сразу, а с интенсивностью

Если запас в момент времени t =0 был s, то спрос к моменту Т может быть меньше или больше запаса, т.е. r £ s и r>s.

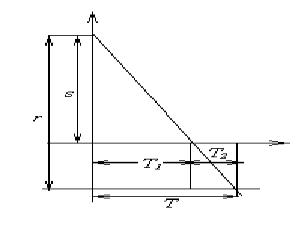
Рисунок 1. График стохастической модели

Рассмотрим эти случаи в отдельности.

а) r<s. В этом случае средний запас (запас, который был + запас, который остался после спроса r) то есть

== s- r. (1)

Эту формулу можно, получить и другим способом

=.

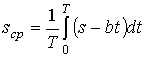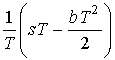При n= r из b T=n=r, и поэтому = s- r, что полностью согласуется с (1).

Поэтому средние затраты на хранение составят:

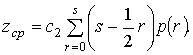(2)

б) r>s. В этом случаи средние затраты состоят их средних затрат на хранение и средних затрат на дефицит продукции [2].

Рассмотрим их в отдельности. Пусть Т₁ время, соответствующее области s >0 и Т₂ - время, соответствующее области s=0 (рис. 1) так, что Т=Т₁+Т₂.

Тогда средний запас с учетом определяется по формуле

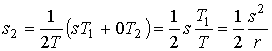. (3)

Этот же результат можно получить и другим способом

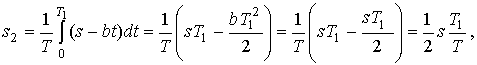
что соответствует (2).

В этом случае затраты на хранение составят

.

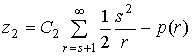Средний дефицит определяется по формуле

(4)

Этот же результат можно получить следующим образом

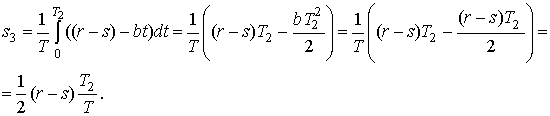
Полагая n=r, имеем

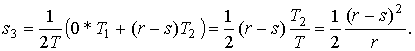(5)

Тогда затраты на дефицит составит

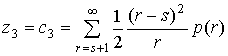. (6)

Можно показать, что оптимальный запас в этом случае определяется как

, (7)

где 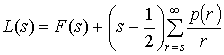- в непрерывном, а

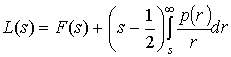- в дискретном случаях.

Пример. Пусть блоки агрегата расходуются со склада равномерно в течение недели. Предполагая, что затраты на хранение одного блока составляет 2 у.е., штраф за дефицит – 16 у.е., а спрос имеет на интервале (0,20) плотность вероятности

, (8)

вычислить общие средние затраты.

Решение. Определим сначала коэффициент r в соответствии с (6):

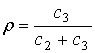=16/18»0.89.

Оптимальное значение запаса находим из условия

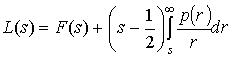=r=0.89 (9)

Здесь

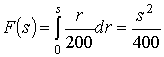, (10)

а второе выражение в (9) равно

===

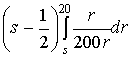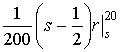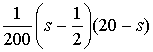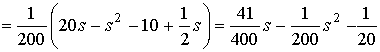. (11)

Поставляя (9) и (10) в (11) имеем

+=0.89,

или

,

или .

Решение этого квадратного уравнения есть

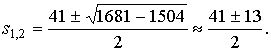
Откуда имеем и .

Таким образом, оптимальным решением является , как принадлежащей интервалу (0,20).

Задачи управления запасами являются одними из самых сложных в математическом смысле. Но эти задачи важны, так как предприятие может терять огромные деньги из-за неправильно рассчитанного сценария управления запасами. Выбор политики управления запасами практически заключается в ответе на один, достаточно простой вопрос: «Какая величина запасов является для предприятия оптимальной?» Очевидно, что запасы нужны для того, чтобы выполнять заказы клиентов на товары в нужном количестве и в установленные сроки. Однако запасы требуют расходов на их содержание, пока они не «дождутся своего часа» и не будут реализованы.

Известные модели управления запасами редко точно описывают реальную систему. Поэтому решение, получаемое на основе моделей этого класса, следует рассматривать скорее как принципиальные выводы, а не конкретные рекомендации. В ряде сложных случаев приходится прибегать к методам имитационного моделирования системы, чтобы получить достаточно надежное решение.

Литература

1. Фасоляк Н.Д. Управление производственными запасами. М.:Экономика, 2012 г., 272с.

2. Хедли Дж., Уайтин Т., Анализ систем управления запасами. Перевод с английского. М.:Наука, 2009 г., 508 с.