Д.ф.-м.н. Срумова
Ф.В.
Таджикский национальный университет
О СПЕКТРАЛЬНЫХ
РАЗЛОЖЕНИЯХ, СВЯЗАННЫХ С ПОЛИГАРМОНИЧЕСКИМ ОПЕРАТОРОМ
Рассмотрены
спектральные разложения, связанные с полигармо-ническим оператором.
Ключевые
слова: полигармонический оператор.
В
работе [1] исследовалась обобщенная проблема
локализации средних Рисса порядка ![]() , отвечающих произвольному самосопряженному неотрицательному
расширению оператора
, отвечающих произвольному самосопряженному неотрицательному
расширению оператора ![]() ,
, ![]() -оператор Лапласа в произвольной
-оператор Лапласа в произвольной ![]() -мерной области
-мерной области ![]()
Рассмотрим
неотрицательное самосопряженное расширение Т оператора ![]() в области
в области ![]() , где
, где ![]() -соответствующее разложение единицы, обладающее ядром
-соответствующее разложение единицы, обладающее ядром ![]() типа Карлемана из
класса
типа Карлемана из
класса ![]() .
.
Пусть
![]()
спектральное разложение любой функции ![]() . Средние Рисса
порядка
. Средние Рисса
порядка ![]() определяются
равенством
определяются
равенством
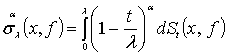 .
.
Теорема.
Пусть функция ![]() удовлетворяет
следующим условиям:
удовлетворяет
следующим условиям:
1) ![]() ;
;
2) ![]() почти всюду в
подобласти
почти всюду в
подобласти ![]() области
области ![]() . Тогда справедливо равенство
. Тогда справедливо равенство
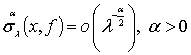
почти всюду в ![]() .
.
Для
доказательства теоремы достаточно установить сходимость интеграла
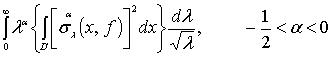 (1)
(1)
где ![]() -произвольная, строго
внутренняя подобласть области
-произвольная, строго
внутренняя подобласть области ![]() . Доказательство сходимости интеграла (1) проводится так же,
как в [1] и [2], только с некоторыми дополнениями,
возникающими при использовании асимптотической формулы среднего значения,
установленной в [3]. Размерность
. Доказательство сходимости интеграла (1) проводится так же,
как в [1] и [2], только с некоторыми дополнениями,
возникающими при использовании асимптотической формулы среднего значения,
установленной в [3]. Размерность ![]() области
области ![]() можем считать
нечетной так же, как в [1] и [2].
можем считать
нечетной так же, как в [1] и [2].
Для получения средних
Рисса
![]()
вводим вспомогательную функцию
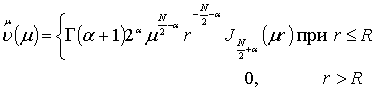
и с помощью
формулы среднего значения подсчитываем образ Фурье этой функции:
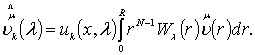 (2)
(2)
где ![]() -ядра упорядоченного
представления пространства
-ядра упорядоченного
представления пространства ![]() относительно
оператора
относительно
оператора ![]() с мерой
с мерой ![]() .
.
Интегрируя
выражение, стоящее в правой части (2), ![]() раз по частям,
получим
раз по частям,
получим
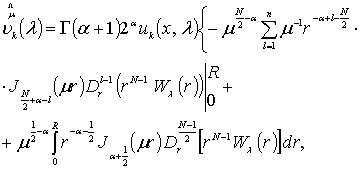 (3)
(3)
где 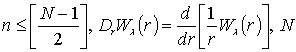 -нечетно. Характер
рассматриваемой особенности обусловливает обращение в нуль результата нижней
подстановки в (3). Умножая равенство (3) на образ Фурье
-нечетно. Характер
рассматриваемой особенности обусловливает обращение в нуль результата нижней
подстановки в (3). Умножая равенство (3) на образ Фурье ![]() , удовлетворяющий условиям теоремы, проинтегрируем полученное
выражение по
, удовлетворяющий условиям теоремы, проинтегрируем полученное
выражение по ![]() от 0 до
от 0 до ![]() , затем просуммируем по всем
, затем просуммируем по всем ![]() от 1 до
от 1 до ![]() В силу свойств
функций
В силу свойств
функций ![]() и
и ![]() и равенства Парсеваля
получим равный нулю интеграл
и равенства Парсеваля
получим равный нулю интеграл
![]()
Лемма.
Пусть
1. ![]() ;
;
2. ![]() в
в ![]() и в пограничной
полосе области
и в пограничной
полосе области ![]() .
.
Тогда
![]()
равномерно в ![]() .
.
Далее
повторяя метод [3], рассуждая, как
автор [1] и принимая во внимание лемму, получим
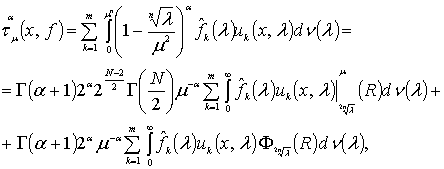 (4)
(4)
где
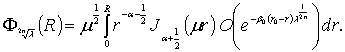
Из
соотношения (4), согласно утверждениям [1], следует, что
достаточно доказать равномерную в ![]() сходимость интеграла
сходимость интеграла
![]()
что устанавливается с помощью неравенства
Коши-Буняковского и равенства Парсеваля при учете, что
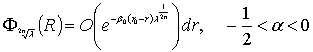 .
.
Литература
1.
В.А.Ильин.
Дифференциальные уравнения, т.6, №7, «Наука и техника», Минск, (1970), 1159-1169.
2.
В.А.Ильин.
Дифференциальные уравнения, т.6, №8, (1970), 1143-1158.
3.
И.А.Шишмарев.
Функциональный анализ и его приложения, т. 3, вып. 4, «Наука», М., (1969)0
69-76.