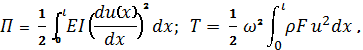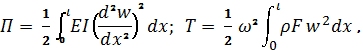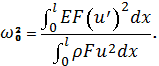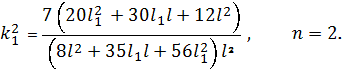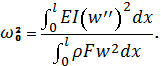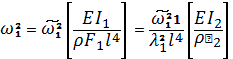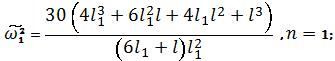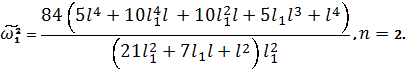УДК.539.3

Трубачев С.И., Колодежный В.А.

ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК СТЕРЖНЕЙ ПЕРЕМЕННОГО СЕЧЕНИЯ

Введение

Стержневые системы и стержни широко применяются в авиационной технике. В процессе работы стержни подвергаются значительному воздействию вибрационных нагрузок, поэтому исследование динамики стержней как постоянного, так и переменного сечения является актуальной задачей. В связи с различными условиями закрепления стержней большое значение имеет численный анализ колебаний указанных конструкций.

Если же решение можно представить в виде ряда функций, то в этом случае предпочтительнее аналитическое решение. Представляет интерес влияние конусности или клиновидности стержня переменного сечения на величину частот продольных или изгибных колебаний.

Постановка задачи

При расчете на вибропрочность основная трудность заключается в определении спектра собственных частот и форм колебаний механической системы и, в общем случае, сводится к известной обобщенной задаче на собственные значения:

(1)

где – множество допустимых функций, – семейство симметричных билинейных непрерывных форм, соответствующих амплитудным значениям потенциальной и кинетической энергии системы, K - матрица жесткостей, M - матрица масс.

При решении задачи численными методами бесконечномерное пространство допустимых функций заменяется конечномерным путем дискретизации системы. При этом задача (1) заменяется приближенной: для заданного конечномерного пространства необходимо найти такие значения , что

(2)

При решении прикладных задач для стержневых систем наибольший интерес представляет несколько наименьших собственных частот и соответствующих им форм колебаний. Таким образом, приходим к неполной задаче на собственные значения. Поскольку эта задача является нелинейной, то целесообразно использовать численные методы.

При продольных колебаниях стержня силы направлены вдоль прямолинейной оси, а напряжения и деформации распределены по площади сечения равномерно. Амплитудные значения потенциальной и кинетической энергии стержня выглядят таким образом:

(3)

здесь Е – модуль Юнга; F – площадь поперечного сечения; - плотность материала; – длина стержня.

Продольные перемещения аппроксимируются линейным полиномом:

(4)

где - перемещения i – го и j-го узлов.

В случае изгибных колебаний стержня амплитудные значения потенциальной и кинетической энергии имеют вид:

(5)

В данном случае для аппрокcимации перемещений используем полином 3-го порядка:

(6)

Для решения задачи (2) использовался итерационный метод покоординатного спуска [2], применение которого позволяет избегать трудностей, связанных с формированием, хранением и оперированием с матрицами масс и жесткостей [2].

При продольных колебаниях стержня в форме клина или конуса первую собственную форму колебаний системы можно представить уравнением

(7)

Физико-геометрические характеристики стержней изменяются по биномиальным законам [3 ]:

(8)

где конусность и приведенная длина соответственно равны [3]:

Для определения основной собственной частоты используется формула Релея:

(9)

Подставляя (7) и (8) в (9), получим соответственно при n=1 для клина и при n=2 для конуса:

(10)

где характеристические числа равны:

(1)

При изгибных колебаниях консольных стержней с биномиальными законами изменения сечений:

(12)

(13)

Первую форму колебаний можно представить приближенным уравнением

,

(14)

которое удовлетворяет только кинематическим граничным условиям:

(15)

Формула Релея при изгибных колебаниях имеет вид

(16)

Подставляя (12) и (14) в (16), получим для основной частоты формулы:

(17)

в зависимости от величины конусности стержня и соотношения
.

В формулах (17) частотный параметр выражается через приведенную и реальную длины стержня так:

(18)

Оценим влияние конусности (клиновидности) стержня на основную частоту на числовых примерах.

Пример 1.

Найти основные частоты продольных колебаний конуса при конусности

По второй формуле (11) получим безразмерные значения характеристических чисел

Подставив в формулу (9), можно получить соответствующие частоты.

Результаты расчета сравнивались с точным решением [3]:

Пример 2.

Определить значения основных частот изгибных колебаний консольного клина при следующих значениях .

По формуле (17) вычисляем значения частотного параметра

Точные значения частотного параметра, полученного в работе [3], следующие:

Из результатов расчета видно, что с увеличением клиновидности (конусности) значения основной частоты тоже увеличиваются.

Выводы

В работе рассмотрены задачи о колебаниях стержневых конструкций переменного сечения. Для решения задач динамики использовался вариационно-сеточный метод. Получены выражения для определения основных собственных частот при продольных и изгибных колебаниях стержней переменного сечения. Результаты расчета сравниваются с точным решением. Исследовано влияние конусности на значения собственных частот, что дает возможность проектировать стержневые конструкции с заданными динамическими характеристиками.

Литература

1. Бабенко А.Е. Застосування і розвиток метода покоординатного спуску в задачах визначення напружено-деформованого стану при статичних та вібраційних навантаженнях. - К.: КПІ, 1996. – 96с.

2. Бабенко А.Е., Бобырь Н.И., Бойко С.Л., Боронко О.А. Применение и развитие метода покоординатного спуска в задачах определения напряженно-деформированного состояния при статических и вибраионных нагрузках. - К.: Инрес, 2005. – 264с.

3. Динник А.Н. Избранные труды. К.: из-во АН УССР, 1965, – 719с.