Технические науки/4. Транспорт

К.т.н. Вуейкова О.Н.

Рудненский индустриальный институт, Казахстан

Исследование зависимости показателей работы карьерных автосамосвалов и автомобильно-экскаваторных комплексов от параметров карьеров

Исследование работы автомобильного транспорта позволило выделить основные факторы, влияющие на показатели работы автосамосвалов в карьерах. К этим факторам относятся [1]:

– скорость движения груженого самосвала;

– скорость движения порожнего самосвала;

– время погрузки самосвала;

– уклон дороги;

– тип и состояние дорожного покрытия;

– профиль трассы.

В результате рассмотрения причинно-следственных связей было установлено, что возникновение простоев автомобильно-экскаваторных комплексов определяется:

– временем выполнения погрузочных операций;

– скоростью движения груженого самосвала.

Время выполнения погрузочных операций зависит от емкости ковша экскаватора V_к, грузоподъемности самосвала q, плотности груза ρ и времени цикла работы экскаватора.

Скорость груженого самосвала зависит от массы груза в транспортном средстве q, уклона трассы и типа дорожного покрытия (w_o+i), коэффициента, учитывающего сложность трассы К_с.

Определение времени погрузки и скорости груженого самосвала для различных вариантов автомобильно-экскаваторных комплексов требует построения математических моделей взаимосвязи между параметрами изучаемого процесса. Существуют различные варианты получения данных для факторных и полиноминальных моделей в зависимости от количества исследуемых факторов, участвующих в исследуемом процессе.

Для получения данных был выбран симметричный композиционный план Бокса второго порядка, состоящий из 14 наблюдений. План Бокс–3 является D–оптимальным, т. е. обеспечивает получение минимума дисперсий всех коэффициентов регрессии; композиционным и обладает свойствами униформности и рототабельности, имеет малое число опытов. Свойство униформности обеспечивает постоянство дисперсии выходного параметра на равных расстояниях от центра эксперимента. Кроме того, данный метод широко используются в исследованиях, и дает хорошие результаты [2, 3].

Серия наблюдений проводилась в трехкратной повторности, которая при проведении активного планирования эксперимента необходима для получения достоверных результатов.

Выходными параметрами являлись:

– время погрузки самосвала – y₁, (мин);

– скорость груженого самосвала – y₂, (км/ч).

Результаты наблюдений по вариантам варьирования записывались в матрицу для проведения математической обработки результатов эксперимента, которая может быть представлена следующей схемой [4]:

– вычисляется среднее значение параметра оптимизации;

– определяется дисперсия каждого опыта матрицы планирования;

– исключаются резко выделяющие оценки, используя критерий Смирнова – Граббса;

– используется критерий Кохрэна для проверки гипотезы однородности дисперсий опыта;

– если дисперсии однородны, то вычисляется дисперсия воспроизводимости эксперимента;

– определяются коэффициенты регрессии b₀, b₁, b₂, b₃, b₁₁, b₂₂, b₃₃, b₁₂, b₁₃, b₂₃;

– находятся дисперсии коэффициентов регрессии;

– рассчитывается среднее квадратичное отклонение коэффициентов регрессии;

– с помощью критерия Стьюдента проверяется статистическая значимость коэффициентов регрессии;

– вычисляется дисперсия адекватности;

– с помощью F – критерия проверяется гипотеза адекватности модели.

В результате произведенных статистических расчетов были получены коэффициенты регрессии. Расчеты и графическая интерпретация результатов реализации параметрических моделей проводились с использованием программ MathCAD14, STATISTICA 6.1, Microsoft Excel 2007.

В уравнении (1) представлена эмпирическая зависимость времени погрузки:

, (1)

где у₁ – время погрузки самосвала, мин.

Анализ уравнений регрессии позволяет выделить факторы, наиболее влияющие на рассматриваемый процесс. Полученные уравнения нелинейны.

Уравнение регрессии (1) характеризует зависимость времени погрузки от объёма ковша экскаватора, грузоподъёмности автосамосвала и плотности транспортируемого груза. Анализируя уравнение (1) установлено, что с увеличением объёма ковша от 6,3 до 27 м³, плотности груза с 2,4 до 3,8 т/м³, грузоподъёмности самосвала от 80 до 180 т время погрузки уменьшается с 6 до 0,8 мин.

Так как представить исследуемый параметр (функцию отклика) в четырехмерном пространстве практически невозможно, анализ его проводили с помощью двумерных сечений поверхности, заключающийся в следующем: анализу подвергались математические модели с закодированными факторами. В уравнении второго порядка подставляются кодированные значения факторов на нулевом уровне, кроме двух изучаемых. В результате получаем выражения, содержащие лишь изучаемые два фактора.

Эмпирическая зависимость времени погрузки от объёма ковша и грузоподъёмности самосвала при среднем значении плотности груза:

₍₂₎

Эмпирическая зависимость времени погрузки от объёма ковша и плотности груза при среднем значении грузоподъёмности:

₍₃₎

Эмпирическая зависимость времени погрузки от грузоподъёмности и плотности груза при среднем значении объёма ковша:

₍₄₎

Эмпирическая зависимость скорости движения груженного самосвала представлена следующей формулой:

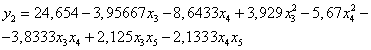, (5)

где у₂ – скорость гружёного самосвала, км/ч.

Уравнение регрессии (5) показывает зависимость скорости гружёного самосвала от грузоподъёмности самосвала, общего сопротивления движения, зависящего от уклона дороги, типа и состояния дорожного покрытия, и коэффициента учёта сложности трассы. Анализируя уравнение (5) выявлено, что с увеличением общего сопротивления движению от 2 до 14%, коэффициента учета сложности трассы от 0,77 до 0,9, грузоподъемности самосвала от 80 до 180 т скорость движения груженого самосвала уменьшается с 34 до 7 км/ч.

Эмпирическая зависимость скорости от грузоподъёмности самосвала и коэффициента учёта сложности трассы при среднем значении общего сопротивления движению:

₍₆₎

Эмпирическая зависимость скорости от общего сопротивления движению и грузоподъёмности самосвала при среднем значении коэффициента учёта сложности трассы:

₍₇₎

Эмпирическая зависимость скорости от грузоподъёмности самосвала и коэффициента учёта сложности трассы при среднем значении общего сопротивления движению.

₍₈₎

Анализ и исследования совокупности технологических и дорожно-транспортных факторов, оказывающих существенное влияние на показатели работы карьерных самосвалов, позволил выявить наиболее значимые: время выполнения погрузочных операций; скорость движения груженого самосвала.

Литература:

1. Мариев, П.Л. Карьерный автотранспорт: состояние и перспективы: учебник/ П.Л. Мариев и [и др.]; отв. ред. А.А. Кулешов. – СПб.: Наука, 2004. – 429 с.

2. Румшинский, Л.З. Математическая обработка результатов эксперимента: учебник / Л.З. Румшинский. – М.: Наука,1971. – 192 с.

3. Спиридонов, А. А. Планирование эксперимента при исследовании технологических процессов / А. А. Спиридонов. – М.: Машиностроение, 1981. – 184 с.

4. Адлер, Ю. П. Планирование эксперимента при поиске оптимальных условий: научное издание / Ю. П. Адлер, Е. В. Маркова, Ю. В. Грановский. – 2–е изд., перераб. и доп. – М. : Наука , 1976. – 279 с.