Математика/4. Прикладная математика

К.ф.-м.н. Зинченко А.Б., Королевская Е.Л.

Южный федеральный университет. Россия

Оптимальные коалиционные структуры для

частного класса нечетких игр

Традиционные модели формирования коалиций разработаны для детерминированной среды. Но в реальной жизни решения часто принимаются в условиях неопределенности. Поэтому, для подстраховки от крупных потерь, агенты иногда не вкладывают все имеющиеся средства или ресурсы в один проект, а распределяют их между несколькими проектами.

Нечеткой коалицией называется вектор FS, где FS_i Î[0,1] - степень участия игрока i в коалиции FS. Величина может быть равной доли времени, которую игрок i готов выделить для участия в коалиции FS, или частью ресурсов, которыми владеет игрок i. Множество называется носителем нечеткой коалиции FS. Если все компоненты вектора FS целые FS_iÎ{0,1}, то нечеткая коалиция FS является характеристическим вектором четкой коалиции . Нечеткие коалиции соответствуют точкам -мерного единичного гиперкуба , а четкие коалиции - вершинам куба.

Нечеткой кооперативной игрой [1] называется пара , где - характеристическая функция, которая каждой нечеткой коалиции FS ставит в соответствие вещественное число и удовлетворяет условию , если .

Характеристическую функцию нечеткой игры обычно трудно описать явно, но можно вычислить ее значения для четких коалиций. В этом случае нечеткую игру определяют с помощью соответствующей четкой игры , где . Рассмотрим некоторые из существующих подходов к решению этой проблемы.

1. Мультилинейным расширением [2] (multilinear extension) четкой игры называется нечеткая игра , где

, .

2. Мультилинейной формой [3] (multilinear form) четкой игры называется нечеткая игра , где

, .

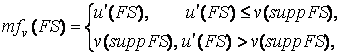
3. Интегральной формой [4] (Choquet integral form) четкой игры называется нечеткая игра , где

, ,

, ,

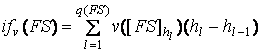элементы упорядочены по неубыванию и обозначены через :

, ,

, .

4. Каноническим представлением [5] игры называется нечеткая игра , где

, .

Пример 1. Пусть и известна характеристическая функция четкой игры

, , , , , , ,

Для нечеткой коалиции с носителем получаем: , , и .

Нечеткой коалиционной структурой [5] называется конечное семейство нечетких коалиций , , удовлетворяющее условию 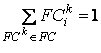, , т.е. компоненты структуры могут пересекаться и суммарная интенсивность участия каждого игрока во всех компонентах структуры равна 1. Множество всех таких структур обозначим через . Вес структуры равен сумме весов ее компонент

, .

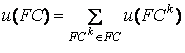Структуру , все компоненты которой – четкие коалиции, будем называть четкой структурой.

Существует также другое определение нечеткой структуры, использованное при обобщении эффективных коалиционных значений. Нечеткой коалиционной структурой в [6] названо разбиение нечеткой коалиции , т.е. , , и для всех ; . Включение означает, что или для всех .

Если структура не сформировалась до начала игры, то желательно найти наиболее выгодную (оптимальную) структуру, т.е. структуру с максимальным весом

.

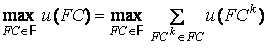Из примера 1 видно, что различные представления нечеткой игры с помощью известной четкой игры могут сильно отличаться и неизвестно, какое из них лучше. Поэтому представляют интерес нечеткие игры, однозначно определенные четкой игрой, а также алгоритмы вычисления их решений.

Предположим, что отличные от нуля доли участия игроков в каждой компоненте структуры одинаковы, т.е.

, .

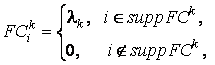
Множество всех таких структур обозначим через . Любую коалиционную структуру можно записать в виде

.

Как отмечено в [7], «... ничто не дает нам повода для экономического объяснения, почему агенты имеют различные уровни принадлежности коалиции». Иногда разная "временная" степень участия агентов в одной и той же коалиции может привести к распаду коалиции.

Предположим также, что

, , , (1)

где - четкая игра, соответствующая нечеткой игре , т.е. для всех непустых четких коалиций . Условию (1) удовлетворяют, например: депозитные игры, в которых ставки по вкладам зависят от срока вклада, но не зависят от величины вклада; частные классы игр коллективного страхования.

Согласно определению нечеткой структуры, количество структур бесконечно и каждая структура может содержать компоненты с одинаковыми носителями. Определим на множестве бинарное отношение

" : « ,

которое рефлексивно, транзитивно и симметрично, т.е. разбивает на классы эквивалентности. Покажем, что каждый класс содержит структуру , все компоненты которой имеют разные носители

; ; . (2)

Подмножество структур из , удовлетворяющих (2), обозначим через .

Лемма 1. Пусть - нечеткая игра, удовлетворяющая (1), и . Тогда существует такая структура , что .

Доказательство. Если , то доказательство закончено. В противном случае, для некоторой пары структурных компонент , , справедливо равенство . Из следует, что и . Рассмотрим семейство коалиций

,

полученное из удалением , и добавлением коалиции , где , . Очевидно, что и . Значит, и . Из (1) следует, что . Повторяя аналогичные преобразования, мы построим необходимую для завершения доказательства структуру, принадлежащую . œ

Покажем, что существует связь между нечеткими структурами, удовлетворяющими (2), и решениями линейной системы с уравнениями и неизвестными.

Лемма 2. Существует взаимно однозначное соответствие между и допустимыми решениями системы

, , . (3)

Доказательство. Пусть - допустимое множество системы (3). Каждый вектор однозначно определяет нечеткую структуру , удовлетворяющую (2). Обратно, пусть . Тогда , , . Вектору соответствует единственный неотрицательный вектор , где

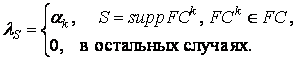
Из следует, что , т.е. . š

Доказанные леммы позволяют свести проблему нахождения оптимальной нечеткой структуры к задаче линейного программирования.

Теорема 1. Пусть - четкая игра, соответствующая нечеткой игре , удовлетворяющей (1). Тогда:

(a) семейство оптимальных структур содержит, по крайней мере, одну структуру ;

(b) существует взаимно однозначное соответствие между оптимальными структурами и оптимальными решениями задачи

, , (4)

где - допустимое множество системы (3).

Доказательство. (a) Рассмотрим произвольную оптимальную структуру , не принадлежащую . Согласно лемме 1 существует такая структура , что .

(b) Значение целевой функции задачи (4) равно весу нечеткой структуры , соответствующей вектору . Пусть - множество оптимальных решений задачи (4). Учитывая лемму 2, получаем, что каждому взаимооднозначно соответствует оптимальная структура . š

Приведенный ниже пример показывает, что, при сделанных предположениях, существуют игры, в которых вес нечеткой структуры больше, чем вес любой четкой структуры и больше веса максимальной коалиции.

Пример 2. Дана игра , где N={1,2,3,4},

, , , ,

для остальных . Все четкие коалиционные структуры (15 структур для игры 4 лиц) имеют вес, не превосходящий . Задача (4) имеет единственное оптимальное решение: , , для остальных , которое определяет нечеткую структуру

с весом .

Литература:

1. Aubin J.P. Cooperative fuzzy games // Mathematics of Operations Research. 1981. No. 6. P. 1–13.

2. Owen G. Multilinear extensions of games // Management Sciences. 1972. Vol. 18. No. 5. P. 64- 79.

3. Meng F.Y., Zhang Q. The Shapley value on a kind of cooperative fuzzy games // Journal of Computational Information Systems. 2011. Vol. 7. No. 6. P. 1846–1854.

4. Tsurumi M., Tanino T., Inuiguchi M. A Shapley function on a class of cooperative fuzzy games // European Journal of Operational Research. 2001. Vol. 129. No. 3. P. 596–618.

5. Mares M., Vlach M. Fuzzy Coalitional structures (alternatives) // Mathware & Soft Computing. 2006. Vol. 13. P. 59-70.

6. Meng F.Y., Zhang Q., Cheng H. The Owen value for fuzzy games with a coalition structure // International Journal of Fuzzy Systems. 2012. Vol. 14. No. 1. P. 22–34.

7. Billot A. Economic theory of fuzzy equilibria // Lecture Notes in Economics and Mathematical Systems. 1992. Vol. 373.