_{Технические науки/12.Автоматизированные системы управления на производстве}

К.т.н. Борин В.С., магістр Тихий А.Б.

Івано-Франківський національний технічний університет нафти і газу, Україна

Математична модель технологічного процесу регенерації диетиленгліколю

Відхилення технологічних параметрів процесу регенерації від заданих норм призводить до зменшення концентрації регенерованого розчину диетиленгліколю, що у свою чергу призводить до неефективного осушення природного газу. Бажану якість (концентрацію) ДЕГу можна отримати тільки при повному інформаційному забезпеченні і оптимальному керуванні технологічним процесом. Одним з можливих шляхів вирішення цієї задачі є автоматизація технологічного процесу регенерації диетиленгліколю з використанням штучних нейронних мереж, яка дасть можливість моделювати за допомогою ЕОМ даний технологічний процес та визначати вплив того чи іншого параметру на процес регенерації. Абсорбція і десорбція – масообміні процеси, які створюють основу абсорбційного розділення нафтових і природних газів. Абсорбційний метод розділення вуглеводневих газів використовується в промисловості для отримання газового бензину і рідких газів (пропан-бутанова суміш). На процес регенерації диетиленгліколю впливають наступні параметри: концентрація і кількість абсорбенту, температура і тиск в десорбері. При осушенні газу до температури крапки роси -10°С використовуються водні розчини гліколю з концентрацією від 99% до 99,5% масових. Концентрація гліколю залежить від ефективності регенерації. При регенерації ДЕГу при 0,1 МПа його концентрація становить 97,5%. Для одержання більш високої концентрації створюють вакуум в десорбері. Концентрацію гліколя вибирають виходячи з умов рівноваги між тиском насичених парів над розчином гліколя і в газі при заданій температурі контакту. Кількість гліколя, який подається в групу абсорберів залежить від тиску і температури в абсорбері (від 25 м3/год до 35 м3/год).

Тиск в десорбері
Зменшення тиску в десорбері покращує процес десорбції поглинутого компоненту (вологи), так як зростає швидкість їх виходу із абсорбенту. Тиск в десорбері складає від 0.11 до 1.1 МПа . При осушенні газу до температури крапки роси -10°С використовуються водні розчини гліколю з концентрацією від 99% до 99,5% масових. Концентрація гліколю залежить від ефективності регенерації. При регенерації ДЕГу при 0,1 МПа його концентрація становить 97,5%. Для одержання більш високої концентрації створюють вакуум в десорбері. Концентрацію гліколю вибирають виходячи з умов рівноваги між тиском насичених парів над розчином гліколю і в газі при заданій температурі контакту. Кількість гліколю, який подається в групу абсорберів залежить від тиску і температури в абсорбері (від 25 м3/год до 35 м3/год).

Температура в десорбері
Підвищення температури сприяє процесу десорбції, так як зростає хаотичний рух молекул поглинутого компоненту і їх відрив від поверхні абсорбенту. Але температура в десорбері обмежується термічною стабільністю абсорбенту і рівна 110…167°С та залежить від типу абсорбенту та способу його регенерації.

Процес десорбції як об'єкт математичного моделювання зображено на рис. 1. Індексами “д” позначено стан газу і абсорбенту при їх вході в десорбер, а “е” - при виході із нього.
Отже, вхідними величинами об'єкта будуть:

– тиск Р_д на вході в десорбер, Па;

– концентрація води в газі Y_д, що поступає в десорбер, кг·моль/кг·моль;

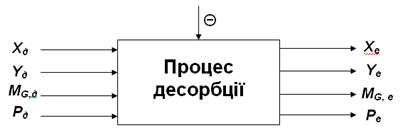
Рисунок 1 – Математична модель процесу десорбції

– концентрація води в абсорбенті Х_д при вході в десорбер, кг·моль/кг·моль;

– навантаження газу на десорбер, MG,д , моль/с;

– температура газу, що поступає в десорбер,К.

Вихідними величинами об’єкта є:

– тиск Ре на виході з десорберу, Па;

– концентрація води в газі Y_е на виході з десорберу, кг·моль/кг·моль;

– концентрація води Х_е в абсорбенті, що покидає установку, кг·моль/кг·моль;

– відбір газу із десорберу, MG,е , моль/с.

Вигляд матричної передавальної функції математична модель тарілки десорбера буде мати наступний вигляд

, (1)

де

;

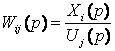– зображення по Лапласу і-тої вихідної величини;

– зображення по Лапласу j-тої вхідної величини.

Для отримання моделі десорберу в цілому враховані зв'язки, які існують між тарілками і граничні умови. Якщо нумерація тарілок ведеться знизу вверх, то на першу тарілку поступає газ в кількості моль/с і вмістом вологи в газі моль·кг/моль·кг; знизу десорбера відбирається насичений абсорбент з вмістом вологи моль·кг/моль·кг. Із N-ої (останньої) тарілки відбирається газ, витрата якого моль/с і вмістом вологи моль·кг/моль·кг; на верхню тарілку поступає абсорбент з вмістом вологи моль·кг/моль·кг.

Оскільки в лінеаризовану модель тарілки входять величини, які

відраховуються від їх усталених значень, то граничні умови для математичної моделі (1) будуть мати такий вигляд:

– для першої тарілки

, , , (1.2)

– для N-ої (останньої) тарілки

, , , (1.3)

Аналізуючи вихідні сигнали бачимо, що при зменшенні вологовмісту диетиленгліколю вологовміст газу, що залишає тарілку, збільшується, а на виходах отримано практично незалежні в часі сигнали, тобто тиск в апараті і витрата газу не залежать від зміни вологовмісту диетиленгліколю. Як бачимо, модель адекватно відображає процес, так як результати на виходах моделі відповідають фізичним основам процесу десорбції.

З практичної точки зору найбільший інтерес для синтезу викликає динаміка колони відносно вхідних u₁ , u₂ (ΔYд, ΔХд) і вихідних Y₁, Y₂ (ΔY_е, ΔХ_е) величин. В такому випадку передавальну матрицю і-ої тарілки отримаємо із матриці шляхом вилучення третього і четвертого стовпця та третього і четвертого рядка. В результаті отримано алгоритмічну структуру десорбера. Кожну тарілку розглянуто як багатомірну ланку з векторним входом і векторним виходом . Динамічні властивості такої ланки характеризуються передавальною матрицею .

Література:

1. Шур А.М., Высокомолекулярные соединения . – М.: Высшая школа, 1981. – 223с.
2. Ульянов В.М., Рыбкин Э.П., Гуткович А.Д. – М.: Химия, 1992. – 202 с.
Штовба С.Д. Проектирование нечётких систем в среде Matlab – М.Горячая линия – Телеком. 100-110 с.

3. Семенцов Г.Н. , Чигур І.І., Шавранський М.В. , Борин В.С. , Фазі – логіка в системах керування : Навчальний посібник. – Івано-Франківськ : Факел, 2002 – 40- 50 с.