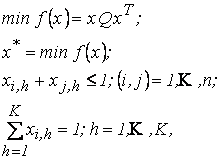Математика. 5.

Скрильник І. І.

Полтавський національний технічний університет імені Юрія Кондратюка

ЗАСТОСУВАННЯ ГЕНЕТИЧНОГО АЛГОРИТМУ ДЛЯ ПОФАРБУВАННЯ N-ДОЛЬНИХ ГРАФІВ

Проблема пофарбування теоретико-графових моделей посідає важливе місце у теорії графів та має особливе прикладне значення. Існує велика кількість задач, для яких може бути побудована еквівалентна модель у вигляді графу, а пофарбування отриманого графу визначає у кінцевому випадку їх розв¢язок. Серед них важливе місце займають задачі машинного генерування розкладів руху міського транспорту, складання розкладів проведення занять у навчальних закладах, планування процесорного часу для виконання комп¢ютерних програм для операційних систем, автоматичне розділення частотних смуг для радіопристроїв, розподілення ресурсів по декільком напрямам для виконання встановлених робіт, розроблення алгоритмів сканування у системах захисту інформації. Інший ряд задач також може бути ефективно розв¢язаний за допомогою пофарбування теоретико-графових моделей, наприклад, у біометрії, теорії кодування, плануванні експерименту, розробленні запам¢ятовуючих пристроїв, у радіоелектроніці тощо. Наведені задачі відносять до NP-складних задач, тому вони вимагають спеціальних методів розв¢язання.

На даний час розроблені евристичні субоптимальні алгоритми, що дають змогу пофарбувати сильно зв¢язані графи з великою кількістю вершин. До даного класу алгоритмів відносять також генетичні алгоритми. Перевагою генетичних алгоритмів є можливість генерування субоптимального розв¢язку при будь-яких накладених обмеженнях. Але їх недоліком є достатньо великий час пошуку розв¢язку. Крім цього, його якість залежить від обраного критерію оптимальності. Тому для підвищення ефективності даної евристичної техніки пошуку розв¢язку та досягнення оптимальності пропонується застосувати комбінований метод, заснований на 0-1 програмуванні та лінійно-квадратичній оптимізації.

Для точного пофарбування графів було запропоновано багато комбінаторних оптимізаційних методів. Широкого розповсюдження набула техніка пофарбування, запропонована Р. Караганом та П. М. Пардалосом. Заслуговують уваги у свою чергу розроблені методи 0-1 програмування Л. Бабелем і Г. Тінгофером, Е. Баласом, Х. Ксю і Чанг Сунг Йю, К. Маніно і А. Сасано, а також Дж. Л. Немгаузером. Відомі також алгоритми пофарбування напівозначеного програмування із використанням розтинів графів. Однак, ефективність наведених методів знаходиться в межах пофарбування графів із 600 – 700 вершинами, оскільки всі вони мають експоненціальну складність. Тому зі збільшенням кількості вершин різко зростає час пошуку розв¢язку. Останнім часом алгоритми оптимізації отримали широке розповсюдження у промисловості, завдяки популяризації такого напряму як комп¢ютерна алгебра, яка має на меті впровадження теоретичних математичних розробок у промислові обчислювальні пристрої.

Нехай на певному обмеженому просторі задано квадратичну функцію . Для будь-якого n-дольного графа G пофарбування є оптимальним, якщо існує мінімум деякої функції та виконується обмеження .

З точки зору мови 0-1 програмування та лінійно-квадратичної оптимізації проблема пофарбування n-дольних графів з накладеними обмеженнями формулюється так:

(1)

де Q – деяка позитивна ненульова матриця. Метою розв¢язання оптимізаційної задачі є відшукання бінарного вектора , такого що .

Дана оптимізаційна задача може бути вирішена при застосуванні точних або евристичних методів. Одним із альтернативних підходів є застосування генетичних алгоритмів, які у загальному випадку представляють собою стохастичну ітераційну оптимізаційну техніку, що ґрунтується на комплексі процедур, які імітують процес виживання популяції в умовах природного середовища. Оптимальне рішення співвідноситься найбільш пристосованому індивіду. Популяція від одного покоління до наступного проходить ряд змін. Операція схрещування служить для отримання нащадків з метою продовження існування початкової генерації. Відбір найбільш пристосованих нащадків контролюється функцією відповідності. Будь-який індивід може бути підданий мутації, що імітує випадкові впливи та генерує новий генетичний матеріал. Загальна структура генетичного алгоритму має наступний вигляд (рис. 1).

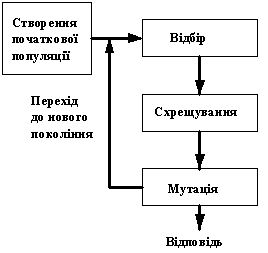
Рис. 1. Узагальнена структура генетичного алгоритму

Оцінювання пристосованості кожного індивіда у поколінні відбувається за допомогою функції відповідності. В нашому випадку будемо застосовувати квадратичну функцію виду . Чим менше значення функції відповідності , тим краще пристосований індивід, тобто тим ближче знаходиться отриманий поточний розв¢язок до оптимуму. В кінцевому випадку необхідно отримати хромосому із найменшим значенням функції відповідності, для якої виконуються обмеження (1).

Зручність застосування генетичних алгоритмів також пов¢язана зі зручністю кодування рішень у хромосомах. На практиці часто застосовують кодування у вигляді одиниць та нулів, отримуючи таким чином бінарні масиви.

У процесі пошуку генетичний алгоритм дозволяє генерувати декілька субоптимальних розв¢язків за одну ітерацію і добитися робастності алгоритму, на відміну від традиційних підходів, які дозволяють лише знайти один розв¢язок протягом ітерації.

ЛІТЕРАТУРА

1. De Wera D. An introduction to timetabling // European Journal of Operations Research. – 1985. - № 19. – P. 151 – 162.

2. Fred C. Chow, John L. Hennesy. Register allocation by priority-based coloring. In Proceedings of the ACM SYGPLAN 84 Symposium on Compiler Construction. - New York: ACM, 1984. – P. 222 – 223.

3. Fred C. Chow, John L. Hennesy. The priority-based coloring approach to register allocation // ACM Transactions on Programming Languages and Systems. – 1990. – № 12(4). – P. 501 – 536.

4. Gamst A. Some lower bounds for a class of frequency assignment problems // IEEE Transactions of Vehicular Echnology. – 1986. - № 35(1). – P. 8 – 14.

5. Arkin M., Silverberg B. Scheduling jobs with fixed start and end times // Discrete Applied Mathematics. – 1987. – № 18.

6. Mikhail J. Atallan. Algorithms and Theory of Computation Handbook. U.S.A, New York: CRC Press, 1999.

7. Grotschel M., Junger M., Reinelt G. An application of combinatorial optimization to statistical physics and Circuit layout design // Operations Research. – 1988. - № 36(3). – P. 493 – 513.

8. Agarwal S., Belongie S. On the non-optimality of four color coding of image partitions // IEEE Proceedings of Int. Conf. Image Processing. – 2002.

9. Алексеев В.А., Носов В.А. NP-полные задачи и их полиномиальные варианты. Обзор. Обозрение промышленной и прикладной математики. - 1997. - т. 4, вып. 2. - с.165 – 193.