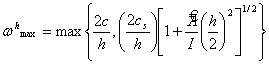Ñåêöèÿ Ìàòåìàòèêà, ïîäñåêöèÿ 4
TIME-STEP ESTIMATES
FOR SOME SIMPLE FINITE ELEMENTS
Sufficient conditions for
stability in finite element analysis may be obtained from estimates of the
maximum eigenvalues of individual elements. Consider some examples. If we
assume a lumped mass matrix for two-node linear rod element, then
|
|
(1) |
where h is the element length and 
is so-called bar-wave
velocity, in which 
is Young’s modulus and
is density. The
critical time step for Newmark method with 
(central-difference
method) is
|
|
(2) |
which is the time required for a bar wave to traverse one element. If we
assume a consistent mass matrix, then
|
|
(3) |
resulting in a
reduced critical time step, viz.,
|
|
(4) |
This result is typical
– Consistent-mass matrices tend to yield smaller critical time steps than
lumped-mass matrices.
For three-node quadratic rod
element, if we assume a lumped mass matrix based on a Simpson’s rule weighting
(the ratio of the middle node mass to the end node masses is 4), we get
|
|
(5) |
|
|
(6) |
Comparison of (6) with (2)
reveals that the allowable time step is about 0.4082 that for linear elements
with lumped mass. This is based upon equal element lengths. Perhaps a more
equitable comparison is one based upon equal nodal spacing. In this case the
ratio doubles to 0.8164, but still the advantage is with linear elements.
For linear beam element
transverse displacement d face rotation are assumed to vary linearly over the
element. One-point Gauss quadrature exactly integrates the bending stiffness
and appropriately underintegrates the shear stiffness to avoid “locking”. We
assume the trapezoidal rule is used to develop the lumped mass matrix. Solution
of the eigenvalue problem results in
|
|
(7) |
where 
is the bar-wave
velocity, 
, the beam shear-wave
velocity, 
is the cross-section
area, 
is the shear area, I is the moment of inertia and 
is the shear modulus.
To get a feeling for these
quantities, we shall take a typical situation. Assume the cross section is
rectangular with depth 
and width 1. This
results in 
and 
. We assume the ratio of wave speeds 
. This corresponds to a Poisson’s ratio of ¼ and shear
correction factor 
, so it is a reasonable approximation for most metals. The
time step incurred by bending mode will be critical when
|
|
(8) |
This would be the
case only for a very deep beam or an extremely fine mesh and is thus unlikely
in practice. The more typical situation in structural analysis is when 
(i.e. very thin beams
or coarse meshing). In this case the critical time step is slightly less
than 
, the time for a bar wave to traverse the thickness. As this
is an extremely small time step, the cost of explicit integration becomes
prohibitive.
Flanagan and Belytshko [1]
have performed a valuable analysis of the one-point quadrature (four-node) quadrilateral and (eight-node)
hexahedron, applicable to arbitrary geometric configurations of the elements.
They obtain the following estimate of the maximum element frequency
|
|
(9) |
where 
, dilatational wave velocity, 
and are Lame parameters
and 
is a geometric
parameter. The estimate (9) leads to a sufficient condition for stability. For
the central difference method (9) results in
|
|
(10) |
As an example of
the restriction imposed by (10) consider a rectangular element with side
lengths 
and 
. In this case (10) becomes
|
|
(11) |
For higher-order elements, there appears that little of a precise nature
has been done. Most results are of the form (10) where the geometric factor is
approximated by trial and error. One would hope that with the aid of the automatic symbolic manipulators,
improved time-step estimates will become available in the ensuring years for
more complex elements, material properties.
REFERENCES
1.D.P.Flaganan,
T.Belytschko, A Uniform Strain Hexahedron and Quadrilateral with Orthogonal
Hourglass Control. – International journal for numerical methods in
engineering.- 1981, v.17.- p.679-706.