Математика/1. Диференціальні та інтегральні рівняння

Колісник Р.С.

Чернівецький національний університет імені Юрія Федьковича

ЕВОЛЮЦІЙНІ РІВНЯННЯ ВИЩОГО ПОРЯДКУ ПО З ОПЕРА-ТОРОМ ДИФЕРЕНЦІЮВАННЯ НЕСКІНЧЕННОГО ПОРЯДКУ

Рівняння з частинними похідними як скінченного, так і нескінченного порядків широко використовуються при математичному моделюванні різних реальних процесів, при розв’язуванні задач математичної фізики, квантової механіки, теорії теплопровідності та тепломасообміну, кристалографії, теорії ядерних ланцюгових реакцій тощо. За допомогою таких рівнянь описуються різні складні явища у сучасному природознавстві, економіці, техніці.

Задача Коші та крайові задачі для рівнянь з частинними похідними мають природну постановку у різних просторах узагальнених функцій, оскільки часто крайові умови мають особливості в деяких точках або ділянках межі. Такі функції допускають регуляризацію у просторах узагальнених функцій скінченного порядку, або їх можна трактувати як узагальнені функції нескінченного порядку, якщо порядок особливостей вищий за степеневий.

При дослідженні проблеми про класи єдиності та класи коректності задачі Коші для рівнянь з частинними похідними зі сталими (або залежними лише від часу) коефіцієнтами широко використовуються простори типу , введені І.М.Гельфандом і Г.Є.Шиловим, та простори типу , введені Б.Л.Гуревичем. Простори типу складаються з нескінченно диференційовних на функцій, поведінка яких та їхніх похідних на дійсній вісі характеризується величинами , де подвійна послідовність задовольняє певні умови (особливо повно досліджено випадок ). Простори типу є узагальненнями просторів типу внаслідок заміни степеневих функцій довільними опуклими, що дозволяє точніше охарактеризувати особливості зростання або спадання функцій на нескінченності.

У працях М.Л.Горбачука, П.І.Дудникова, О.І.Кашпіровського, С.Д.Івасишена, Л.М.Андросової, В.В.Городецького, В.П.Лавренчука, І.В.Житарюка, О.Г.Возняк, В.А.Літовченка встановлено, що простори типу - простори, топологічно спряжені до просторів типу , - є природними множинами початкових даних задачі Коші для широких класів рівнянь з частинними похідними скінченного порядку, при яких розв’язки є нескінченно диференційовними функціями по просторових змінних. В.В.Городецьким, О.В.Мартинюк, О.М.Ленюком аналогічні результати у просторах типу встановлені для певних класів рівнянь з частинними похідними нескінченного порядку (еволюційні рівняння, які містять оператор диференціювання нескінченного порядку, або оператор диференціювання–Бесселя нескінченного порядку). У працях [1,2] побудовані класи цілих функцій (простори типу ), які спадають на дійсній вісі при швидше, ніж ; при цьому простори типу , а також простори типу утворюють певні підкласи просторів типу . У цих працях розвивається теорія задачі Коші для одного класу рівнянь з частинними похідними з початковими умовами з просторів типу . Природно виникає питання про одержання аналогічних результатів для еволюційних рівнянь вищого порядку по з оператором диференціювання нескінченного порядку. У роботі дається відповідь на поставлене питання у випадку задачі Коші для вказаних рівнянь у просторах узагальнених функцій типу (аналітичних функціоналів).

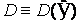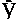Нагадаємо, що символом позначається множина всіх фінітних нескінченно диференційовних на функцій. Сукупність всіх лінійних неперервних функціоналів на 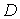зі слабкою збіжністю позначається через 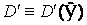. Елементи 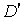називаються узагальненими функціями. Сукупність узагальнених функцій з 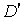, які обертаються в нуль на півосі 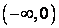, позначається символом 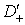. Розглянемо узагальнену функцію 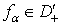, яка залежить від параметра 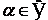, і визначається формулою

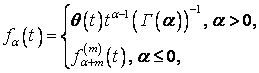
де – найменше серед натуральних чисел таке, що , – функція Хевісайда. За допомогою будуються оператори . Оскільки , то оператор при називають оператором дробового диференціювання.

Нехай – простір введений в [1]. Розглянемо рівняння

(1)

з початковою умовою

. (2)

Тут – простір, топологічно спряжений до , – ціла та дробова частини числа, – оператор дробового диференціювання, який діє по змінній у просторі .

Теорема. Задача Коші (1), (2) коректно розв’язна в класі узагальнених функцій . Розв’язок при кожному фіксованому належить до простору і подається у вигляді

де ( – фундаментальний розв’язок задачі Коші (1), (2)).

Література:

1. Городецький В.В., Колісник Р.С. Про одне узагальнення просторів типу // Науковий вісник Чернівецького університету: Зб. наук. пр. Вип.134. Математика. – Чернівці: Рута, 2002. – С. 30-37.

2. Городецький В.В., Колісник Р.С. Оператори диференціювання нескінченного порядку у просторах типу та їх застосування // Доп. НАН України. – 2004. – № 10. – С. 14–19.

3. Гельфанд И.М., Шилов Г.Е. Пространства основных и обобщенных функций. –М.: Физматгиз, 1958. – 307с.