Экономические науки/10.Экономика предприятия

К.э.н. Уразбахтина Л.Р., м. Маннанова З.С.
Казанский государственный энергетический университет, Россия

Методы и модели в управлении производственными запасами предприятия

Эффективное управление запасами предприятия в современных условиях рынка - необходимое условие повышения эффективности бизнеса, создания, развития и реализации конкурентных преимуществ предприятия, которое осуществляется при помощи научно разработанных путей и методов оптимизации систем управления производственными запасами.

Создание производственных запасов и управление ими являются неотъемлемой частью многих видов деятельности в производстве и логистике. Широко известно, что создание крупных запасов приводит к увеличению затрат на складирование и блокированию капитала. С другой стороны, решение о сокращении запасов приводит к необходимости более частых заказов на товары, которые обычно увеличивают общие расходы на их доставку, сохраняя при этом риск нехватки товаров (например, «нет в наличии»). Таким образом, появляются некоторые вопросы: что является оптимальным запасом, как часто должны выполняться заказы и в каком объеме должны быть заказаны товары.

Чтобы найти основные ответы на эти вопросы, существуют методы и модели управления запасами. Основываясь на полученных результатах этого проблемного научно-практического поля, компьютерные программисты разрабатывают практические алгоритмы для управления запасами в системах производства и логистики.

Количество возможных вариантов того, как организовать системы управления запасами, практически бесконечно, потому что каждый вариант может быть смешан со многими ограничениями, встречающимися в реальной жизни, и это означает, что количество возможных вариантов управления запасами составляет тысячи.

В принципе, для количественного исследования систем управления запасами могут быть реализованы два класса моделей: аналитические (чисто математические) и моделирующие (компьютер). Оба cвязаны с математическими моделями, и каждая из них основана на конкретной теоретической (концептуальной) модели.

В классе аналитических моделей имеется большое количество модификаций.

Простая модель - вывод формулы Вильсона, является единственным продуктом статической модели с непосредственным пополнением запасов и отсутствием дефицита.

Самая простая модель - монопродуктовая статическая модель. Простая модель управления запасами в характеризуется тремя свойствами: постоянное время спроса; немедленное пополнение; отсутствие дефицита. Уравнение полностью описывает рассматриваемую систему хранения запасов. Оптимизация заключается в выборе наиболее экономичного количества запасов. Чем они меньше, тем чаще новые запасы должны быть размещены. Поскольку расходы зависят от частоты заказов и объема укомплектованных запасов, значения должны определяться из условия баланса между видами расходов. В некоторых случаях, например, когда предприятие одновременно производит и потребляет продукты, запасы пополняются постепенно, не сразу. Это означает, что в данном случае, одна часть производственной системы работает как поставщик для другой части системы, которая играет роль потребителя. Чаще всего, скорость производства преодолевает скорость потребления.

Есть много модификаций этой модели, наиболее известными из которых являются следующие:

- Модель с учетом потерь от дефицита.

- Модель с постепенным планом пополнения запасов.

- Модель с учетом дефицита счета с планом пополнения запасов.

- Многоотраслевая модель заказа.

- Модель с учетом оптовых скидок.

- Модель с учетом налогового учета НДС.

Между тем, задача управления запасами может и не иметь существующей аналитической модели. В этом случае единственная возможность изучить эффективность управления запасами заключается в реализации одного из типов компьютерного моделирования. Моделирование позволяет не только отразить почти любые особенности системы управления запасами, но определить критерии оптимальности системы на основе финансовой модели процесса доставки любой сложности.

Одним из перспективных имитационного моделирования управления запасами является симплекс-метод, представляющий собой разновидность линейного программирования.

Идея симплекс-метода состоит в том, чтобы перейти от одного базового допустимого решения (то есть одной крайней точки) набора ограничений задачи в стандартной форме к другой таким образом, чтобы непрерывно уменьшать значение целевой функции до минимума.

Симплекс-метод позволяет получить матрицу решения транспортной задачи бесперебойности поставок с учетом стоимости самой поставки. В общих затратах времени на движение товара от первичного источника сырья до конечного потребителя всего лишь 2-5% занимают затраты времени на собственно производство, а 95% – на хранение, складские, транспортные и другие логистические операции. Так решается вопрос бесперебойности пополнения производственных запасов предприятия, а также снижения транспортных расходов, что является важным резервом снижения себестоимости продукции и дополнительным фактором роста экономической эффективности предприятия. Нахождение оптимальных схем и маршрутов доставки позволит сократить финансовые и временные логистические затраты.

Примером типичной транспортной задачи (ТЗ), решаемой симплекс-методом, является распределение (транспортировка) продукции, находящейся на складах, по предприятиям-потребителям. Стандартная ТЗ определяется как задача разработки наиболее экономичного плана перевозки продукции одного вида из нескольких пунктов отправления в пункты назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.

Решается ТЗ как двухиндексная задача линейного программирования.

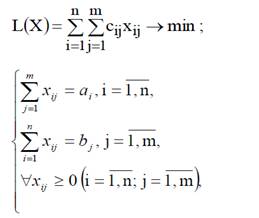
(1)

где L(X) – транспортные расходы на перевозку всей продукции;

xij – количество продукции, перевозимой из пункта отправления в пункт назначения;

сij – тариф (стоимость) перевозки единицы продукции из пункта отправления Аi в пункт назначения Вj;

ai – запас продукции в пункте отправления Ai;

bj – спрос на продукцию в пункте назначения Bj.

Целевая функция представляет собой общие транспортные расходы на осуществление всех перевозок в целом. Первая группа ограничений указывает, что запас продукции в любом пункте отправления должен быть равен суммарному объему перевозок продукции из этого пункта. Вторая группа ограничений указывает, что суммарные перевозки продукции в некоторый пункт потребления должны полностью удовлетворить спрос на продукцию в этом пункте. Наглядной формой представления симплекс-модели является транспортная матрица (табл. 1.1).

Таблица 1.1

Общий вид симплекс-матрицы

Пункты отправления, Ai	Пункты потребления, В;				Запасы, ед. прод.
	B1	В2	…	Вm
A1	С11 [руб./ед. прод.]	С12	…	С1m	а1
А2	С21	С22	…	С2m	а2
…	…	…	…	…	…
Аn	Cnl	Cn2	…	Сnm	аn
Потребность ед. прод.	b1	b2	…	bm

Из симплекс-модели следует, что сумма запасов во всех пунктах отправления должна равняться суммарной потребности во всех пунктах потребления. Если это условие выполняется, то симплекс-модель называется сбалансированной, в противном случае – несбалансированной. В случае, когда суммарные запасы превышают суммарные потребности (или наоборот), необходим дополнительный фиктивный, т.е. реально не существующий, пункт потребления (пункт отправления), который будет формально потреблять (отправлять) существующий излишек (недостаток) продукции.

Таким образом, можно сделать вывод о том, что оптимальный уровень запасов материальных ресурсов позволяет повышать качество принимаемых управленческих решений при формировании необходимых размеров запасов материалов на промышленных предприятиях, а также минимизировать материальные запасы, что в результате способствует высвобождению оборотных средств предприятия. Практическими методами для принятия решений по управлению производственными запасами может служить симплекс-метод линейного программирования, позволяющий обеспечивать предприятие запасами МТЦ в режиме бесперебойности и с учетом экономии затрат на их транспортирование.