Левицький Г.В.,
Лєпа Є.В.
Херсонський
національний університет
ДОСЛІДЖЕННЯ МЕТОДІВ
РОЗРАХУНКУ НАДІЙНОСТІ КОМПЮТЕРНИХ МЕРЕЖ
В наш час, коли
інформація відіграє визначну роль у розвитку суспільства та визначається як
найцінніший ресурс, постає питання щодо встановлення підходів стосовно
зберігання та передачі інформації. Всі ці функції покладені на комп’ютерні
мережі різної області дії (персональні, локальні, глобальні мережі), через які
здійснюється доступ до інформації та забезпечується її надійність
(кластеризація, резервування тощо). Тож як ніколи актуальним постає питання
щодо забезпечення надійності комп’ютерних мереж, підтримання їх працездатності
на протязі довгого часу та відновлення робочого стану у разі втрати окремих
функціональних вузлів.
Під надійністю
ми розуміємо властивість об'єкта зберігати в часі у встановлених межах значення
всіх параметрів, що характеризують здатність виконувати необхідні функції в
заданих режимах і умовах застосування, технічного обслуговування, зберігання і
транспортування. Розрахунок надійності комп’ютерної мережі дозволить мати
представлення стосовно тривалості роботи системи за різних умов, допоможе дати
оцінку тих чи інших способів підвищення безвідмовності та живучості мережі.
Розрізняють
наступні методи розрахунку надійності:
-
структурні методи;
-
логіко – імовірнісні
методи;
-
метод дерев відмов;
-
метод Марковського
моделювання.
Структурні
методи є основними методами розрахунку показників надійності в процесі
проектування об'єктів, що піддаються розділенню на елементи, характеристики
надійності яких в момент проведення
розрахунків відомі або можуть бути визначені іншими методами.
У логіко –
імовірнісних методах вихідна постановка задачі та побудова моделі
функціонування досліджуваного системного об'єкта або процесу здійснюється
структурними і аналітичними засобами математичної логіки, а розрахунок
показників властивостей надійності, живучості та безпеки виконується засобами
теорії ймовірностей.
Дерево відмов
(аварій, подій, наслідків, небажаних подій) лежить в основі логіко –
ймовірнісної моделі причинно – наслідкових зв'язків відмов системи з відмовами
її елементів і іншими подіями.
Метод Марковського моделювання ґрунтується на Марковських
процесах, що являють собою спеціальний вид випадкових процесів. Він може бути використаний для моделювання випадкової
системи, що змінює стан відповідно до правила переходу, що залежить від
поточного стану.
Комп’ютерні мережі володіють рядом
особливостей, зокрема вони мають багаторівневу структуру та велику
кількість функціональних вузлів. Тому
для оцінки надійності пропонується розглянути мережу на системному рівні
деталізації, у вигляді функціональних блоків, а не у вигляді блоків, які б
характеризували кожну конкретну апаратну одиницю у структурі мережі.
У якості прикладу розглянемо типову корпоративну мережу, що включає в себе такі елементи як: локальна обчислювальна мережа центрального обчислювального комплексу (далі – ЦОК), середовище передачі даних (далі – СПД), центру управління мережою (далі – ЦУ). У центральному вузлі розташовуються розрахунковий центр і центр ресурсів. В ньому зосереджуються корпоративні дані і ресурси, щоб забезпечити функціонування завдань прикладної інфраструктури корпоративної мережі. У складі даного комплексу встановлюються необхідні сервери для виконання всіх видів прикладної обробки даних. Незважаючи на досить-велику кількість підсистем, неважко помітити, що всі вони виконують одну з трьох функцій: передачу, обробку або зберігання даних. Таким чином, в корпоративної мережі реалізуються три основні функції - передача даних, обробка даних, зберігання і відновлення даних. Функції передачі даних виконують мережу доступу і транспортна мережа. Функції обробки та зберігання даних виконує центральний обчислювальний комплекс. У разі відмови однієї з підсистеми корпоративна мережа перестає виконувати основні функції.
Від складної схеми КС можна перейти до моделі надійності з трьох підсистем.
Така модель можна представити у вигляді схеми, показаної на рисунку 1.1.

Рисунок 1.1 - Послідовна модель надійності КС
Працездатність елементів у корпоративних мережах контролюється
централізовано, центр управління використовується для виявлення відмов та їх
усунення. У той же час при його відмові функції передачі та обробки даних
продовжують виконуватися. Для аналізу надійності такої підсистеми розглянемо
модель функціонування з незалежними відмовами підсистем, яку умовно представимо
у вигляді моделі, зображеної на рисунку
1.2.

Рисунок 1.2 – Модель мережі з залежними відмовами
Кожна з підсистем являє собою апаратно-програмний комплекс, відмова такої
підсистеми може виникнути внаслідок різноманітних причин. Однак, з точки зору
користувачів мережі, не важливо, внаслідок яких саме відказів виникають простої
мережі. Уявлення комп’ютерної мережі у
вигляді функціональних блоків дозволяє розглянути як програмні, так і механічні відхилення.
Кожна із систем може знаходитися в одному з двох станів: працює, не працює.
При відмові від СПД або ЦОК система переходить в неробочий стан. При відмові ЦУ, система працює, однак, у разі відмови СПД і ЦОК при непрацездатному ЦУ, відновлюється спочатку ЦУ, потім не працює сама СПД або ЦОК. Опис можливих станів системи приведено в таблиці 1.1.
Таблиця 1.1.
Можливі стани системи
|
Стан СПД |
Стан ЦОК |
Стан ЦУ |
Стан мережі |
Стан системи |
|
1 |
1 |
1 |
0 |
СПД працює, ЦОК працює, ЦУ працює, мережа працює |
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
1 |
2 |
СПД працює, ЦОК відказав, ЦУ працює, мережа не працює, відновлюється і повертається в робочий стан |
|
1 |
1 |
0 |
3 |
СПД працює, ЦОК працює, ЦУ не працює, мережа працює, відновлюється ЦУ, перехід в стан 1 |
|
0 |
1 |
0 |
4 |
СПД відказала, ЦОК працює; ЦУ не працює, мережа не працює, відновлюється ЦУ, відновлюється СПД і повертається в робоче стан 1 |
|
1 |
0 |
0 |
5 |
СПД працює, ЦОК відмовив, ЦУ не працює, мережа не працює, відновлюється ЦУ, відновлюється ЦВК і мережа повертається в робоче стан 1 |
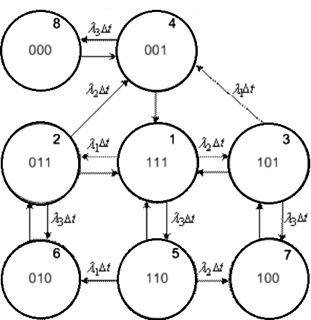
На рисунку
1.3. зображено граф можливих станів системи за проміжок експлуатації Δt, інтенсивність відмов СПД, ЦВК і ЦУ відповідно
дорівнюють λ1, λ2 та λ3.
Рисунок 1.3 – Граф станiв мережі
Висновки:
1.
Для розрахунку
показників надійності будь – якої
системи спочатку виконується побудова її математичної моделі системи. Це
виконується для того, щоб враховувати характеристики системи, зокрема, у
розглянутому випадку, отримано граф можливих станів системи.
2.
В якості основного
показника надійності роботи комп’ютерної
системи зазвичай розглядається коефіцієнт готовності. Оцінка надійності при
цьому проводиться враховуючи закони розподілу часу відновлення компоненту
системи та інтенсивність відмов даного
елементу.
3.
Провівши розрахунки,
можна виконати оцінку ефективності будь — якого із елементів системи та
розробити алгоритми щодо підвищення їх надійності та безвідмовності.