д.т.н., професор Лукашенко В.М., к.т.н.,
доцент Уткіна Т.Ю.,
ст. викладач Рудаков К.С., магістрант Тіщенко В.О.,
аспірант Гавриш А.В., аспірант Романович Р.Я.
Черкаський державний технологічний університет,
Україна
ДОСЛІДЖЕННЯ КОМПОНЕНТІВ ЦИФРОВОГО РЕВЕРБЕРАТОРА
Використання реверберації є складовою частиною загальної обробки аудіо
сигналів при записі мови, співу, музики, та також створенні різних шумових
ефектів. При розробці цифрового ревербератора (ЦР) важливу роль відіграють
параметри саме процесора обробки звуку, такі як напруга живлення та діапазон
температур, при яких вони можуть працювати. Також, час затримки –
безпосередньо впливає на те, яким буде вихідний звук, і коефіцієнт нелінійних
спотворень, що впливає на суму спектральних компонентів вихідного сигналу.
Вплив даних факторів на продуктивність та надійність пристрою зручно
визначати за допомогою методів, що дозволяють одночасно аналізувати кілька
величин відповідних параметрів. До того ж, економічна ситуація в країні лише
погіршується, а промислові моделі ревербераторів досить дорогі.
В роботах Колєснікова Є. А.,
Котова С. Т., Барчукова В. С., Рибакова О. С., Калінчука В. Г., Бажинова А. В.,
Дьякова А. В. та ін., висвітлюються питання,
присвячені методам підвищення якості проектування ЦР. Але недостатньо
розкрито, як з великої кількості ЦР вибрати найкращу модель за багатьма
параметрами одночасно [1-3]. Враховуючи, що багатокритеріальність і візуалізація
сприяють скороченню часу при проектуванні нових пристроїв, то дослідження
взаємозв’язків визначених параметрів ЦР на їх основі, є актуальною
задачею.
Метою роботи є дослідження компонентів на базі метода
візуалізації для визначення найкращих моделей цифрових ревербераторів за
допомогою багатокритеріальної моделі на основі теорії неповної подібності та
розмірностей.
Для досягнення даної мети необхідно:
-
створити перелік сучасних
фізичних моделей ЦР та їх основних параметрів і синтезувати узагальнену
математичну модель взаємозв’язків визначених параметрів за їх відсутності;
-
створити перелік величин, які
мають суттєвий вплив на експлуатаційну технологічність компонентів і розробити
умовні критерії подібності на основі теорії неповної подібності та розмірностей
за визначальними величинами й надати їм фізичне тлумачення;
-
побудувати образно-знакову
модель залежності між умовними критеріями подібності в безрозмірних
координатах;
-
провести аналіз
образно-знакової моделі і визначити найкращі варіанти ЦР на основі
конкретних вимог замовника.
Рішення поставленої задачі. Оскільки основними технічними параметрами
ЦР (табл. 1), які впливають на експлуатаційну технологічність
комплексів обробки звуку є: напруга живлення, робочий температурний діапазон,
час затримки сигналу та коефіцієнт нелінійних спотворень, то визначати найкращу
модель ЦР за багатьма параметрами пропонується за допомогою взаємозв’язків
визначених параметрів [1].
Таблиця 1
Перелік сучасних фізичних моделей ЦР та їх основних параметрів
|
Тип пристрою Параметри |
HT 8970 |
РТ 2399 |
MN 3005 |
MN 3007 |
MN 3011 |
|
№ |
1 |
2 |
3 |
4 |
5 |
|
Діапазон напруги живлення, В |
0,3…6 |
4,5…5,5 |
15…16 |
15…16 |
15…18 |
|
Діапазон коефіцієнта нелінійних спотворень, % |
0,7…1,5 |
0,3…1 |
1…2,5 |
0,5…2,5 |
0,4…2,5 |
|
Інтервал затримки сигналу, мс |
29,8…327,6 |
31,3…342 |
20,5…204,8 |
5,12…51,2 |
1,99…166,4 |
|
Діапазон робочих температур, °C |
-20…70 |
-20…75 |
-20…60 |
-20…60 |
-20…70 |
Синтезується узагальнена математична модель для визначення
взаємозв’язків між технічними параметрами, що вказані в табл. 1, яка
приймає наступний вигляд [2]:
![]() (1)
(1)
де ![]() – мінімальні
і максимальні значення вхідної напруги;
– мінімальні
і максимальні значення вхідної напруги;
![]() – мінімальні
і максимальні значення робочої температури;
– мінімальні
і максимальні значення робочої температури;
![]() – мінімальні
і максимальні значення часу затримки сигналу;
– мінімальні
і максимальні значення часу затримки сигналу;
![]() – мінімальні
і максимальні значення показника коефіцієнту нелінійних
спотворень.
– мінімальні
і максимальні значення показника коефіцієнту нелінійних
спотворень.
Аналіз формули (1) показав, що відсутнє аналітичне вираження
залежності між параметрами, які досліджуються в табл. 1. Тому рішення
поставленої задачі пропонується на основі фізичного моделювання, теорії
неповної подібності та розмірностей і евристичного методу. Для цього
створюється перелік визначальних величин з основних технічних
параметрів ЦР та критеріальне рівняння на основі умовних критеріїв.
Умовними критеріями подібності називаються прості безрозмірні степеневі
комплекси, які сформовані з визначальних величин.
Тому, при використанні теорії неповної подібності, визначальних величин
по даним табл. 1, формули (1) і використанні евристичного методу
визначення умовних критеріїв подібності, рівняння приймає наступний вигляд:
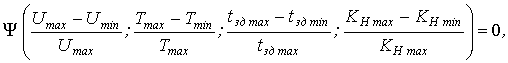 (3)
(3)
де 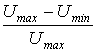 – безрозмірна
величина, що характеризує діапазон вхідної напруги, в
якому може працювати ЦР;
– безрозмірна
величина, що характеризує діапазон вхідної напруги, в
якому може працювати ЦР;
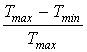 – безрозмірна
величина, що характеризує температурний діапазон, в
якому може працювати ЦР;
– безрозмірна
величина, що характеризує температурний діапазон, в
якому може працювати ЦР;
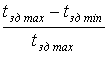 – безрозмірна
величина, що характеризує діапазон часу затримки сигналу, з яким може
працювати ЦР;
– безрозмірна
величина, що характеризує діапазон часу затримки сигналу, з яким може
працювати ЦР;
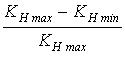 – безрозмірна
величина, що характеризує діапазон коефіцієнта нелінійних
спотворень, з яким може працювати ЦР.
– безрозмірна
величина, що характеризує діапазон коефіцієнта нелінійних
спотворень, з яким може працювати ЦР.
На основі властивостей теорії неповної подібності та розмірностей
будуються образно-знакові моделі залежності між визначеними умовними критеріями
подібності в безрозмірних координатах. Це надає можливість наочно порівняти
технічні параметри пристроїв та визначити ті, що як найкраще відповідають
вимогам замовника [4].
Графік побудованої знакової моделі залежності основних технічних
параметрів у безрозмірних координатах представлений на рис. 1.
 251698688251699712251700736251702784251703808251704832251728384251729408
251698688251699712251700736251702784251703808251704832251728384251729408
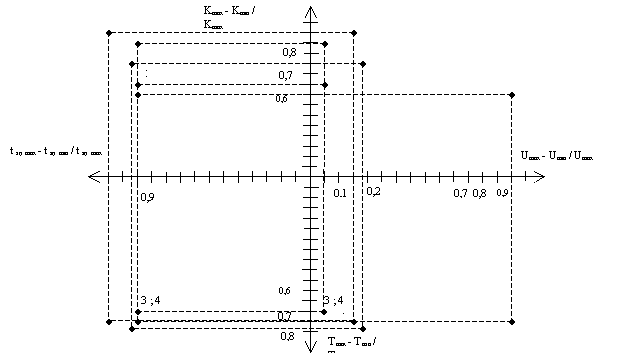
Рис. 1. Знакова модель залежності
основних технічних параметрів
сучасних фізичних моделей ЦР в безрозмірних координатах
Примітка:
цифри 1, 2, …, 5 відповідають цифрам в табл. 1.
На рис. 1 представлена образно-знакова модель залежності
основних технічних параметрів для різних моделей ЦР в безрозмірних
координатах, з якої видно, що ЦР 1 має найкращий показник по напрузі
живлення, а також високі значення показників робочої температури і часу
затримки сигналу. Також ЦР 1 має найнижчий показник коефіцієнта нелінійних
спотворень, але так як коефіцієнт нелінійних спотворень – негативна величина,
то чим менше його значення – тим краще. ЦР 2 має найширший температурний
діапазон та доволі високий показник часу затримки сигналу. ЦР 5 має
найкращий показник часу затримки сигналу і найгірший показник коефіцієнту
нелінійних спотворень серед усіх моделей ЦР. Отже, розглянуті моделі ЦР
мають доволі високі показники часу затримки сигналу та діапазону робочої
температури і переважна більшість – низькі показники напруги живлення (2,
3, 4, 5) та коефіцієнту нелінійних спотворень (2, 4, 5). ЦР 3 має найнижчі
показники з усіх, не враховуючи його показник коефіцієнта нелінійних
спотворень.
Висновки:
1.
Проведено дослідження на базі
багатокритеріального методу аналізу фізичних моделей ЦР, що ґрунтується на
властивостях теорії неповної подібності та розмірностей і фізичному
моделюванні, відмінною особливістю якого є висока швидкість визначення ЦР
з найкращими технічними параметрами, завдяки візуалізації.
2.
Процедура візуалізації
дозволила швидко обрати відповідний
ЦР (HT 8970) та визначити напрям його удосконалення (за показником коефіцієнта нелінійних спотворень), при цьому одночасно
враховані взаємозв’язки між багатьма параметрами.
Література:
1.
Лукашенко В. М.
Критериальные зависимости для выбора оптимальных параметров коммутаторов
/ В. М. Лукашенко // Вісник ЧІТІ. – 2000. –
№ 3. – С. 65–70.
2.
Эффективный метод анализа
сложных моделей и их компонентов для специализированного лазерного
технологического комплекса / А. Г. Лукашенко,
Д. А. Лукашенко, И. А. Зубко, В. А. Лукашенко,
В. М. Лукашенко // Вісник ЧДТУ. – 2011. –
№ 4. – С. 42–47.
3.
Трьохкоординатна знакова
модель для визначення перспективних мікропроцесорних компонентів за багатьма
параметрами / К. С. Рудаков, Р. Є. Юпин,
А. Г. Лукашенко, В. А. Лукашенко, В. М. Лукашенко
// Вісник ЧДТУ. – 2012. – № 1. – C. 28‑31.
4. Рудаков К. С. Двоквадрантна
образно-знакова модель визначення ефективного маршрутизатора
/ К. С. Рудаков, В. М. Лукашенко,
Т. Ю. Уткіна // Вісник ХНУ. – 2015. – № 2. –
С. 150–156.