Ктн, доцент Василенко В

Ктн, доцент Василенко В.С., Гасімов Ф.М.О.

Національний авіаційний університет (НАУ) України

завадостійкий код умовних лишків

На сьогоднішній день завдання контролю та поновлення цілісності інформації в сучасних інформаційно-комунікаційних системах та мережах є важливим як ніколи. Вся інформація в нашому житті повільно перетікає в мережу, і без сумніву є ті, хто захоче цим скористатися змінивши або видаливши інформацію яка нам потрібна. Одним з найвідоміших механізмів поновлення інформації вважають формування хеш-функції на етапі запису інформації. Під хеш-функцією розуміється відображення довільної інформації що контролюється,в образ фіксованої невеликої довжини за правилами того, чи іншого перетворення. Також існує механізм блочного контролю цілісності інформації, коли контрольована інформація розподіляється на блоки – базові та узагальнені кодові слова.

Метою статті є розроблення та аналіз механізму формування контрольних ознак, які є стійкими щодо несанкціонованої модифікації даних, або їх спотворення.

Для цього автори пропонують такий завадостійкий код, у якому для формування контрольних ознак можна використовувати певну множину змінних секретних констант і щоб цей код міг забезпечити необхідну цілісність інформації від її несанкціонованої зміни (модифікації) або спотворення.

Для цього пропонуються використати можливості теорії лишкових класів по відношенню до інформації, наданої у вигляді кодів незалежно від систем числення, а також застосування основ, які можуть бути використані як секретні елементи і забезпечити за рахунок цього формування контрольних ознак, які є стійкими до розкриття. Очікується забезпечення цілісності отриманої інформації за рахунок виявлення та виправлення спотворень, які виникають в результаті впливів природних та штучних завад, а отже, забезпечення стійкості цієї інформації до навмисної модифікації або спотворення.

Спотворення інформації, тобто її несанкціонована зміна, можливе на будь-якому етапі її перебування у обчислювальних мережах: при зберіганні, передачі або обробці. Наразі в сучасних інформаційних системах розповсюдженим є забезпечення цілісності інформації із застосуванням завадостійких корегуючих кодів. Цей метод знайшов широке застосування в протоколах передачі даних. При цьому при одночасному застосуванні перемежування потрібної глибини забезпечується можливість збільшення довжини інформаційних об’єктів, цілісність яких контролюється. Але більшість завадостійких кодів не мають можливості використовувати закриті (таємні) алгоритми чи їх константи, і тому не виключають можливостей будь-якої модифікації інформаційних об’єктів. Як код, що має можливість використання секретних параметрів пропонуються узагальнений завадостійкий корегуючий код на базі теорії лишкових класів, так званий код умовних лишків (ЛУ - код).

В системі лишкових класів будь-яке число представляють у вигляді набору лишків від розподілу цього числа на набір взаємно простих чисел, які мають назву основ системи числення – p_i, де і = 1, 2, …, n, n – кількість таких основ. Вибір величини n здійснюють з умови, яка викладена нижче. Тоді

А = α₁, α₂, …, α_n, (1)

де α = А – [А/p_i]·p_i, а позначка [А/p_i] означає операцію розрахунку цілої частини від дробового числа А/p_i. При цьому між числом А і його уявленням () існує взаємна однозначна відповідність при умові, що

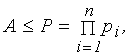
де Р – діапазон представлення або робочий діапазон інформаційних об’єктів (чисел).

Величина α_і є значенням і - тої групи двійкових розрядів, яка не перевищує величини відповідної основи p_i.

Основною властивістю системи лишкових класів (СЛК) є те, що вона дозволяє нам ефективніше виявляти і виправляти спотворення в групах двійкових розрядів, тобто в узагальнених символах. Якщо ми введемо ще одну, надлишкову, основу р_к, то уявлення А в розширеному діапазоні
R = P·р_к, у вигляді

А = α₁, α₂, …, α_n, α_k, (2)

де α_ĸ – лишок по основі р_к, утворює завадостійкий код.

При побудові таких завадостійких кодів слід забезпечити наступні умови: при p_k > p_n будь-яке спотворення в одному з лишків (узагальненому символі) α_і може бути виявленим, а при p_к > 2·p_n·p_n₁, де p_n, p_n₁– найбільші із основ, може бути і виправленим.

У такого коду є свої недоліки. По-перше можливі спотворення знаходяться і виправляються (спотворений символ поновлюється) тільки в тому випадку, якщо спотворено лише один з символів α_і, тобто спотворення повинні бути фіксованими в межах однієї із груп розрядів. Цей недолік є притаманним будь-якому коду і тому усувається всім відомими способами, наприклад, застосуванням декореляції, глибина якої повинна бути не менше ніж 2. По-друге, є також недолік, пов’язаний з необхідністю роботи з числами в системі числення в залишкових класах. Цей недолік достатньо просто усунути в ЛУ–коді, який вводиться таким чином.

Код деякого числа А – базове кодове слово (БКС), представляють в будь-якій системі числення, зокрема позиційній, наприклад двійковій. Розбивають цю послідовності певним (у загальному випадку довільним) чином на n узагальнених символів, як і для решти узагальнених кодів.

Код кожного i-го узагальненого символу розглянемо як s - значний розряд α_i, який може приймати будь-яке з s значень від 0 до (s - 1), де s = 2^b. Код цього символу вважається лишком деякого умовного числа А по основі p_i. Оскільки величина α_i, як елемент початкового числа

0 ≤ α_i ≤ s - 1,

а як лишок від ділення А на p_i

0 ≤ α_i ≤ p_i,

то для представлення коду будь-якої групи у вигляді лишку по основі p_i необхідно, щоб виконувалася наступна умова

p_i > s – 1,

інакше в групу із b розрядів може бути записаним код α_і ≥ p_i, що в лишкових класах не допустимо.

При такому підході будь-які комбінації початкового коду числа А “вписуються” в систему числення з основами p_i (і = 1, 2, ...). Якщо ми розширимо систему основ на надлишкову основу p_k і для одержаного набору умовних лишків α_i(і = 1, 2,...) розрахуємо надлишковий умовний лишок α_k,то на одержане нами умовне число

А’ = α₁, α₂, …, α_n,α_ĸ (3)

розповсюджується усі можливості СЛК по виявленню і виправленню спотворень, тобто одержаний код (3) має всі властивості коду (2), але останній код може бути застосованим для будь-якої двійкової послідовності, а не тільки по відношенню до чисел в лишкових класах. Таким чином ми можемо усунути другий недолік коду (2).

ЛУ-код дозволяє нам знаходити і виправляти b − розрядні пакети спотворень, згруповані в межах будь-якого з n узагальнених символів і потребує при цьому надмірність біля r ≈ 2b + 1 двійкових розрядів (оскільки р_k ≈ 2р_nр_n₊₁, то r = [log₂р_k] + 1). В конкретних випадках ця надмірність може відхилятися в ту або іншу сторону, що залежить також від алгоритмів кодування-декодування.

Оскільки в основі ЛУ-коду лежать властивості СЛК, то в цьому коді ми можемо використати і відомі алгоритми кодування-декодування.

Це стає можливим завдяки тому, що спотворення в одній з груп розрядів α_і переводить початкове число з робочого діапазону [0, P = ) в діапазон [P, R = p_k·Р), що призводить до збільшенню початкового числа
А’ < Р на деяку величину l_i·R_i. Де l_i і R_i = R/ p_i – цілі числа. А якщо вихідне число

А = α₁, α₂, …, α_i,…,α_n, α_k

є спотвореним по основі p_i і прийме вид

= α₁, α₂, …, ,… ,α_n,α_ĸ

де

= {α_i + Δα_i } (mod p_i),

то це буде еквівалентним наступному перетворенню

= (α₁, α₂, …, α_i,…,α_n, α_k) + (0, 0, …, Δα_i, …,0, 0) =

= (α₁, α₂, …, {α_i + Δα_i } (mod p_i),…,α_n1, α_k).

Рис. 1. До виходу спотвореного числа за межі робочого діапазону

При цьому величина спотворення перевищує величину робочого діапазону Р:

ΔА = (0, 0, …, Δα_i, …,0, 0) > Р,

оскільки тільки число виду

ΔА = l_i·R_i = l_i·R/p_i

має всі лишки, окрім лишка по основі p_i, такими, що дорівнюють нулю. Але
ΔА = l_i·R_i > P = R/p_k тобто, навіть при l_i = 1 величина R/p_i > R/p_k по тій причині, що p_k > p_i.

Відтак, якщо сума = А’ + ΔА > Р, а саме наше число вийшло за межі робочого діапазону Р, попало в діапазон [P, R) стало спотвореним. Коли ж спотворення відсутні (ΔА = 0) прийняте число < Р, не стає спотвореним. Завдяки цьому факту ми можемо здійснювати кодування(формування надлишкових символів) та декодування(виявлення наявності викривлень та можливого їх корегування). Це дає нам можливість унеможливити несанкціоновану модифікацію інформації, що циркулює в телекомунікаційних мережах.

Висновки. Автори запропонували в задачах контролю цілісності інформаційних об’єктів використання завадостійкий код умовних лишків, що робить несанкціоновану модифікацію інформації неможливою. За рахунок цього очікується підвищення рівня захисту цілісності інформації, що циркулює в телекомунікаційних системах і мережах.

Література:

1. Василенко В.С. Технології забезпечення доступності інформаційних об’єктів при застосування багаторівневої частотної модуляції. / В.С.. Василенко, О.Ю. Цибенко // ISSN 1561-6940, Pridneprovsky research journal. Научный журнал. – Наука и образование, Днепропетровск – № 11 (147). − 2013. – С. 54 − 61.

2. Василенко В.С. Теория информации и кодирования. / В.С. Василенко, О.В. Дубчак // Монографія, ISBN 978−3−659−15893−3, LAMBERT Academic Publishing, Saarbrücken, Deutschland. − 2013. – с. 494

3. Василенко В.С. Василенко В.С. Прикладная теория информации и кодирования. / В.С. Василенко, Е.В. Дубчак // Монографія, ISBN 978-3-659-45467-7, LAMBERT Academic Publishing, Saarbrücken, Deutschland. − 2013. – с. 129.

4. Целостность и доступность информационных объектов. / В.С. Василенко, О.Я. Матов // Монографія, ISBN 978−3−659− 47333−3, LAMBERT Academic Publishing, Saarbrücken, Deutschland. − 2013. – с. 95.