Bukhovets A.G. Dr. Sc. (Eng.), Biryuchinskaya T.Y. Cand. Sc. (Phys.-Math.)

Department of Applied Mathematics, Voronezh State Agrarian University named after Emperor Peter I, Michurina str., 1, Voronezh, 394087, Russia

Tel.: +7 473-253-73-69; fax: +7 473 253-86-51

E-mail address: abuhovets@mail.ru, bir_tat@mail.ru

PROPERTIES OF SETS GENERATED BY RANDOM ITERATED FUNCTION SYSTEMS

Abstract: Fractal properties of attractors for the randomized systems of iterated functions are considered in the work. The special attention is given to characteristic lines of these sets connected with algorithms generating them

Keywords: Fractal analysis, random iterated function systems, simulating fractal sets.

Highlights:

· Constructions fractal sets by means of as random iterated function systems, and an alternative method by construction of the matrix which lines represent the sums of in a random way taken members of absolutely converging number are considered.

· The basic properties received fractal sets such as powers, perfection, resolvability, convergence are considered.

1. Introduction

Random iterated function systems (RIFS) represent one of the most significant achievements in the theory of fractals being at the same time a component in the theory of dynamic systems [1]. Mathematical aspects of this concept have been first developed by Hutchinson and directly used in the theory of fractals [2]. However, the performed investigations were as a rule executed within the frameworks of classical approach, i.e. without the study of the properties of passage to the limit and intermediate results of RIFS performing. In this work it was proposed to consider the results RIFS execution from the two different points of view – classical one and constructive one. So, for example, during the study of problems of the convergence for a certain RIFS it shall be specially stipulated each time if we deal with an actual infinity meaning the finalized and realized one or the infinity is considered as a potential one, otherwise as a possibility to continue the calculations in principle for an arbitrary long time. In other words the result of the study is to some extent determined by the fact how the analysis will be made – either constructive approach is applied or consideration is performed within the frameworks of the classical analysis – for example, from the viewpoint of the naive set theory. An approach proposed in the present work when both different points of view were taken into account, describes behaviour of a system in that special cases that seem to be very important in the practical conditions when a solution does not depend on the details of the initial and boundary conditions but the system is still far from the limiting states. In fact, the sets obtained as a result of RIFS represent some intermediate-asymptotic solution.

Moreover, in our work a special attention was tended to notice the alternative way of constructing fractal sets based on the generalization of approach for summation of series with random signs of terms [4]. The use of such approach which is to some extent dual (alternative) relative to the routine way of constructing fractal sets makes it possible to perform the evaluation of RIFS parameters when solving some practical problems.

2. Realization of the random iterated function systems

Let’s first introduce the following definitions:

1. Proto-fractal means a set Z – discrete or continuous one generating fractal set during RIFS execution. To realize this procedure it is necessary to preliminarily specify some probability measure P(Z) and determine the value of parameter µ.

2. Pre-fractal X is a countable set of points which appears as a result of RIFS realization.

3. Fractal is a limiting set composed of all the possible points that can appear (potentially) during RIFS execution.

To realize certain RIFS it is proposed to apply the following procedure [3]. Let’s assume that a certain value of some parameter µ is specified and some set of points is determined in R^P Euclidean space that we further name a proto-fractal as agreed above; let a probability distribution is determined upon this proto-fractal. Initial point is determined in a random order. In order to obtain the points of simulated set the following procedures are successively executed:

1. According to the predetermined distribution measure the point of proto-fractal is chosen;

2. Coordinates of point are calculated by the formula

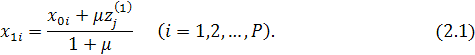
Next, the obtained point is taken as an initial one and items 1-2 are repeated as many times as many points of the generated set are required. As a result of execution of this procedure a set of points is obtained and named pre-fractal as it was agreed above, just similar to the determination of precompact. Fractal term should be used to designate a limiting set. The iterated procedure described above will be specified as F1.

Computation of pre-fractal points can be also organized in another way. Without limiting of generality and for convenience let’s consider the execution of this procedure in one-dimensional case. Let is an initial point of the procedure that can be taken randomly. Then a successive execution of the iterated procedure can be represented as follows:

(2.2)

……………………………………………………………………………. ��(…ξ(ξ(ξ

The obtained expression represents notation of Homer's method for the n-the polynomial of �� variable without a free term with the coefficients which were obtained by selection according to the predetermined measure (Р) from an aggregate of points of the proto-fractal at each iteration step multiplied by the coefficient µ. Removing the brackets we obtain the following equality

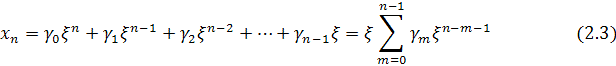
Then rewrite equation (1), changing the order of summation and make an upper estimate of the sum

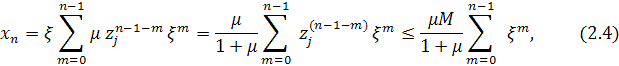
where for µ ≥ 1.

For value one can obtain more accurate estimate by rearranging of series terms and collecting terms relative to Z_j

,

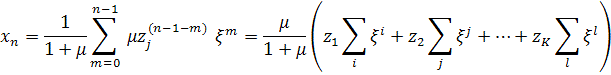or

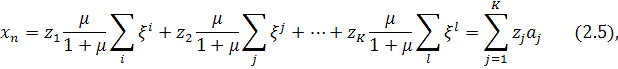
where

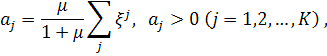
and while summation in some certain terms is performed over the number of proto-fractal points chosen according to the algorithm represented in item 2.

Note that from (2.5) follows – each point of the obtained pre-fractal is a linear combination of proto-fractal points.

Thus, constructing of pre-fractal for a predetermined set of , distribution of the probability values and the value of in fact means the execution of the following operations:

1. According to the distribution of К values of totals are calculated formed from the elements of absolutely convergent series of the type

The obtained К values are recorded in line as the elements of matrix, where N is the number of the required pre-fractal points, К is the number pre-fractal points. The rule of assignment for i-th term of series to some of the summands can be an arbitrary one. In our numerical experiments it was usually assumed that all of the series terms could be equiprobably included into the sum of any summand. However, it is not difficult to provide any other relation of the probabilities.

2. Matrix A obtained as a result of the calculations is multiplied by matrix, composed of pre-fractal points. Result of the product – matrix will be a list of coordinates of the points for pre-fractal X in the specified space.

Thus, if is obtained then construction of pre-fractal means simply multiplication of the matrices. Such way of constructing of the pre-fractal set that is to some extent reciprocal to that one described above will be further noted as F2.

Multiplicative representation fractal sets X=A×Z allows to receive further statistical estimations of a proto-fractal using this parity.

Let's notice, that procedure F1 represents some generalisation of procedure of M. Barnsley known under the name «chaos game» [4], and procedure F2 somewhat it is possible to consider as analogue of the Bak–Tang–Wiesenfeld sandpile model that allows to use further it in modelling the process self-organized criticality.

Equivalence of these two proposed procedures for construction of the fractal sets F1 and F2 is supported by the graphical results obtained under their execution for the same input parameters.

3. The power of sets generated by RIFS

Let’s consider an issue related to the power of sets obtained during execution of RIFS. Cantor discontinuum (С-set) is known to be a classical and universally recognized example of the fractal set [1]. Among a lot of the equivalent determinations for C-set let’s choose the one that seems to be the most convenient one in this situation meaning that it corresponds to our purpose to the highest extent. Usually C-set is determined algorithmically, i.e. geometrical (or, more exactly, mechanical) way for constructing of this set is proposed. It is based on a successive elimination of the central third for the unit segment and next the study of its properties is performed. Examples for construction of the fractal sets with different dimensions according to this principle are given in [1].

However, there is another approach. For example, in [4] one can see: «Cantor discontinuum can be determined as a set of all numbers involved between zero and one, that can be written in ternary notation using only ''0'' and ''2''». There are also alternatives where C-set is written directly with the help of «0» and «1» digits; this allows to make a direct conclusion that this set has a power of continuum, since this record represents binary notation of any number involved within the unit interval starting from zero.

Let’s show that a set of points obtained as a result of F1 procedure execution, can be homeomorphically mapped to C-set. In this case it is convenient to use symbol dynamics method [5], based on the coding of each path of a dynamic system by a sequence of symbols.

Let is a predetermined pre-fractal including K points and so we have K different digits, respectively. Let’s agree that if Z_m point was chosen at the k-th step of F1 procedure execution then in the numeral of the number Y_k = 0,y₁ y₂…y_k m digit will be logged at k-th position, i.e. we suppose that y_k = m. Obviously, 0< Y_k <1. Then each set obtained as a result of F1 procedure execution can be aligned in biunique correspondence with a number Y_k E_k, recorded in the numerical system with the base number K but without the use of 0 digit in the numerals. Such a set corresponds to Cantor set [1]. Note, that here an assumption is made that each number in the chosen numerical system has a single notation.

The presented construction means that the obtained sets E_k are enumerative, i.e. if one knows a sequence of digits in the number Y_k = 0,y₁ y₂…y_m it is always possible to construct sequence E_k and vice versa. With this presentation of the sets of points for pre-fractal it is easy to show using Cantor’s diagonal method, that in case of accepting the idea of actual infinity the limiting set – fractal has a power of continuum.

Really, assuming the contrary idea, i.e. that the limiting set is a countable one let’s set down successively all the numerical sequences corresponding to the obtained sets at each step of the procedure. Due to the countability this procedure can be really made. After that let’s make a new number W = 0,w₁w₂… w_k… basing on the known principle: w₁ can be any of the chosen digits of numerical system except the first digit of the number Y₁, i.e. w₁ ≠ y₁. The second digit w₂ can be any of the chosen digits of numerical system except the second digit of the number Y₂ and so on. Obviously, the obtained number W differs from Y1 by the first digit, from Y₂ – by the second one and so on. In other words, the number W will not coincide with no one of the numbers presented in the enumeration. In turn, it means that the assumption on the countability of the set of points for the fractal as in the limiting set is not true; it means that this assumption is false.

In a certain sense, if to draw analogy with the numbers arranged within the unit segment, the points obtained with the use of the procedure F1 can be compared with the presentation of rational numbers of the segment while the rest ones that can be potentially obtained – compared with irrational numbers. In this case both situations are very similar: rational numbers are sufficient for the practical applications (results of the procedures F1), while theoretical reasoning require the use of irrational numbers and, hence the points that can be obtained in principle. By the matter, note that this theoretical construct, for example, to explain why Serpinsky’s triangle obtained with the use of F1 procedure for µ=1 provides the fractal dimension equal to 1,58 [7], and it is in a good correspondence with theoretical value of dimensionality equal to .

Thus, there is a pre-fractal – the sets of , obtained during the execution of the procedure F1 are countable and the limiting set has the power of continuum.

4. Solvability and enumarability of sets obtained by RIFS

Let’s consider the problem of solvability of the fractal set of points. In other words, the problem implies the possibility to answer the question – if the given point is a member of a set Х, i.e. to determine if the set is a decidable one.

In order to determine the membership of point to a set Х it is convenient to consider that was obtained during execution of the procedure F2. In this case the following representation occurs, according to (2.5)

where .

Statement 1. In order the set would be a set obtained by F2 procedure it is necessary and sufficient that among its elements there was a dominating element [9], i.e. the element , with the value exceeding the sum of values for all the rest elements.

◄ Necessity. Let and the following equality occurs

Then the first term of this series is equal to , while the sum of all the rest series terms is

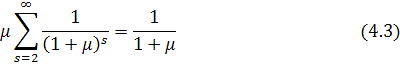
For the given value of the following inequality is obvious

Sufficiency. Let elements be the totals of randomly selected elements of the series (4.2) and the value of is a dominating one

Below one can see that in this case the value of parameter can be determined in such a way that the corresponding procedure F2 results in the execution of the relation (4.5).

In fact, from the condition of dominance and relation of it follows that , and , respectively. In this case, if a set of was obtained using procedure F2, must involve the first term of series (4.1). To check if it is true let us consider the value of the first term in this series as a function of parameter µ

Obviously f(1)=1/2, , and, hence, for the value of the first term in this series is no less than 1/2, so, condition (4.5) is always satisfied. ►

Thus, in order to obtain all points of the pre-fractal related to Z_m, it is sufficient to determine the dominance component and arbitrarily generate the rest of the components from the terms of series (4.2). Obviously, in this case all of the rearrangements for the elements form a group of transformations.

5. On the perfection of fractal sets

If one considers E_n from the viewpoint of the countable axiomatics and relies on the finite conclusions then the set of obtained for a finite number of steps can be represented as a sum of the countable number of one-point sets and each one of them has null Lebesgue measure. Due to the countable additivity of the measure set has a null measure as well, and topological dimension of such set will be equal zero. However, considering of the limiting set – fractal, as it was mentioned above, allows to come to some other conclusion: namely, the limiting set can have the measure different from zero [9].

In order to investigate the limiting properties of the obtained sets they were considered as the actually infinite ones; it means that an infinitely great amount of pre-fractal points has been already obtained. In other words, at least one point with the required properties among a set of the points obtained with the use of F1 or F2 procedures can always be found. Let’s show that within the frameworks of this assumption the following statement is true

Statement 2. The obtained limiting set is a closed one.

◄ To prove this let’s show that within any ε-vicinity of the arbitrary point Х, being a member of the limiting set there is at least one point Х^*≠Х, that is also a member of this limiting set. In other words, a set of fractal points involves all of its limiting points, i.e. it is a closed one set. Let’s consider the points obtained with the use of F2 procedure. According to (2.5) we have

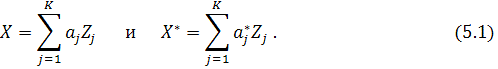
For convenience let us confine our consideration by the case , . Then, in order that Х and Х^* were both within the ε-vicinity, the following ratio must be satisfied

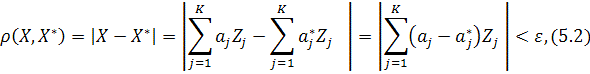
where ε is an arbitrary positive number. Consider as a vector with the coordinates obtained with the use of F2 procedure keeping in mind that the order separation in (2.5) is known. Next, find the first element among the terms of series (4.2) that obeys inequality

where and also set the coordinate , related with . Let is chosen as the vector determined according to the following rule

i.e. differs from а only by the fact that the element is transferred from the cell with number i to the cell with number i-1. Then

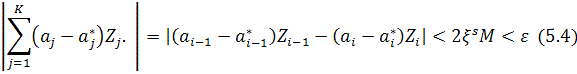
Thus, knowing the order of constructing of arbitrary point for fractal Х using F2 procedure it is possible determine at least one point of the same fractal for any ε-vicinity.►

It is obvious that in the presented proof an actual infinity of the points of fractal set has been essentially applied.

As it is seen from the proof, any point of the fractal set Х is a limiting point. And this means that a set Х is a perfect one [10].

6. Study of the convergence for RIFS procedures

Let’s consider the problem concerning convergence of the procedure for constructing of pre-fractal . The ways for specifying of the finite and infinite mathematical objects are known to be different. To determine finite sets it is sufficient a simple enumeration of the elements in a set, while in case of the infinite sets this way seems to be unreasonable. In the latter case an algorithm for the computation of the terms in this set is usually provided, as, for example, in case of numerical sequences , or the property characterizing the relation of the objects to the set, for example, continuity of the function. While considering infinity of a set , potential infinity is meant i.e. a possibility to infinitely continue the process while in the second case an actual (realized) infinity is usually meant.

Obviously, F1 should be considered as a potentially unlimited constructive process. In this case it is important to divert from the principal incompleteness of this process but at the same time just the possibility of constructive obtaining of the investigated mathematical objects makes them very convenient for the application of finite-dimensional methods of analysis.

Thus, consideration of the results of the F1 procedure’s execution ca be represented in the following form

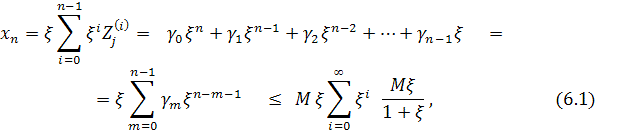
where , , , and without the loss of generality it is reasonable to consider all Z_j to be positive. Considering of as a particular sum of an absolutely convergent series allows to state as if the series , considered as actually infinite mathematical object in case it is a majorized one converges as well. However, this statement is not true – that is clearly seen from the geometrical presentation of the results of numerical experiments. The matter is that sequence is not a fundamental one due to the randomness of choice of the elements.

In fact, as it was shown above the generated fractal set is a perfect one. In particular, it means that each point if this set is a limiting one. Thus, it is impossible to fix a single limit of the generated sequence (6.1).

The situation here is approximately the same as in the case of Specker sequence. Specker [11], as it is known, gave an example which showed that a theorem on the convergence of monotonously varying sequence within the frames of the constructive interpretation is false.

The sequence obtained as a result of F1 procedure can be related to the sequences of Specker type. It is limited and without the loss of generality it may be considered as non-negative one. Homeomorphism with Cantor discontinuum – and classical Specker sequence in the process of its realization represents just the points of Cantor discontinuum – emphasizes the topological commonality of these sequences. In fact, Specker sequence can be represented as a result of RIFS execution with proto-fractal and arbitrary values of as well as the value of µ=2. Results of the execution of F1 and F2 procedures with the given parameters illustrate well this fact. With such approach Specker sequence enumerates Cantor’s set, or, more exactly, its fractal limit. However, in the obtained sequence of, unlike of the Specker one, there exist subsequences converging to separate proto-fractal points – for example, at the constant choice of the point in F1 procedure.

Conclusion

Practical application of RIFS results to a high extent depends on the main properties of sets obtained during the execution of the corresponding procedure. However, certain properties characteristic for the results are considerably determined by the interpretation of the computational experiment. In case when the resulting set is considered from the viewpoint of constructive approach, a set obtained as a result of numerical RIFS realization is

· A countable set of a null Lebesgue measure;

· Sequence of Specker type arranged inside the linear shell for the proto-fractal points.

At the same time the limiting set – fractal is

· A set with a power of continuum;

· Countable set, i.e. compact and closed one,

· In general, having Lebesgue measure different from null.

The final choice of the properties is determined by appropriateness of the use of results. For example, the use of F1 and F2 procedures for the approximation problems of the point sets assumes consideration of the pre-fractals properties. At the same time comparison of these two different fractal sets requires the knowledge of just the limiting properties of these objects.

References

1. Crownover R.M. Introduction to Fractals and Chaos. Boston: Jones & Bartlett • 1995.

2. Hutcthinson J.E. Fractals and Self Similararity. Indiana University Mathematics Journal, vol. 30, #5, 1981, pp. 713-747.

3. Barnsley M. Fractals Everywhere. Academic Press, 1988.

4. Morozov A.D. Introduction to fractals theory. – Moscow-Izhevsk, 2002, 160 p.

5. Bowen R. Methods of symbolic dynamics. – M.: Mir, 1979, 244 p

6. Bukhovets A.G. Modeling of fractal structures of the data / Bukhovets A.G., Bukhovets E.A. // - Management systems and information technologies, № 3(33), 2008, P. 4-7.

7. Bukhovets A.G. Semenov M.E. Determination of fractal data dimensions in the classification tasks. Review of applied and industrial mathematics – M.; 2006, v. 13, iss. 1, p. 86.

8. Bukhovets A.G., Biryuchinskaya T.Ya., Bukhovets E.A. The use of fractal models in classification problems. Management systems and information technologies, 2009б 3.1(37), P. 117-121.

9. Bukhovets A.G., Biryuchinskaya T. Ya., Korablina N.A. Dominate factors in modeling a fractal structure. Economical prognosis: models and methods. Proceedings of VI International theoretical and practical conference on 6 of April 2010 – Voronezh: VGU, 2010.- v.1., p. 61-66.

10. Gelbaum B.R., Olmsted J. M. H. Counterexamples in Analysis. 1964.

11. Specker E. Nicht konstruktiv beweisbare Satze der Analysis, Symbolic Logic, 14 A949, 145—158.