Математика/5. Математическое моделирование

К. п. н. Коробская А. В.

Харьковский национальный университет имени В. Н. Каразина, Украина

Включение оператора интегрирования в узел

Теория модельных представлений несамосопряженных операторов играет важную роль при изложении новых аналитических подходов к решению задач теории спектральных представлений. Так, предпосылками к развитию современных направлений функционального анализа послужили работы по теории характеристических функций [1; 2], функциональных моделей [3], аналитических функций [4], спектральных представлений несамосопряженных операторов [5; 6]. В связи с этим возникает необходимость в изучении различных типов линейных операторов и их свойств.

В [1; 2] был изучен оператор изометрии, исследование которого послужило основой спектрального анализа несамосопряженных операторов. Отметим, что оператор, который представляет собой линейную комбинацию оператора интегрирования и его сопряженного, в данном контексте не изучался.

Рассмотрим в оператор вида , где , . Оператор ограничен. Действительно, рассмотрим 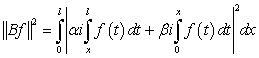, тогда

.

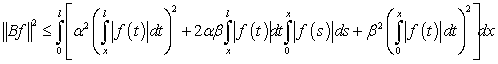В силу неравенства Коши-Буняковского получаем следующую оценку: 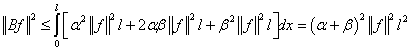. Т. е. доказано, что , где .

Легко видеть, что сопряженный оператор к имеет вид: .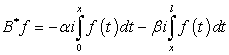

Включим оператор в узел . Найдем :

.

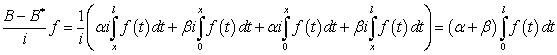Т. е. , где , и , а , и , где – постоянная на функция равная .

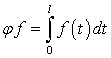Итак, получена следующая теорема.

Теорема. Операторный узел для 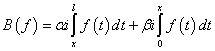имеет вид: , где , .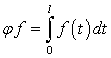

Таким образом, в данной работе изучен оператор 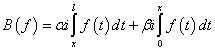, который является линейной комбинацией оператора интегрирования и его сопряженного, доказана его ограниченность, представлен сопряженный к нему оператор. Осуществлено включение данного оператора в узел и описаны параметры узла.

Литература:

1. Лившиц М. С. Операторы колебания волны. Открытые системы / М. С. Лившиц. – М., 1966. – 298 с.

2. Лившиц М. С. Теория операторных узлов в гильбертовых пространствах / М. С. Лившиц, А. А. Янцевич. – Х. : Изд-во Харьк. ун-та, 1971. – 160 с.

3. Надь Б. С. Гармонический анализ операторов в гильбертовом пространстве / Б. С. Надь, Ч. Фояш. – М. : Мир, 1970. – 431 с.

4. Гарнет Дж. Ограниченные аналитические функции / Дж. Гарнет. – М. : Мир, 1984. – 496 с.

5. Бродский М. С. Треугольные и жордановы представления линейных операторов / М. С. Бородский. – М. : Наука, 1969. – 287 с.

6. Золотарев В. А. Аналитические методы спектральных представлений несамосопряженных и неунитарных операторов / В. А. Золотарев. – Х. : [ХНУ], 2003. – 342 с.