АССИММЕТРИЧНАЯ ЛОКАЛИЗАЦИЯ
В МАГНИТНОЙ СТРУКТУРЕ
Акимов М.Л.,
Поляков П.А., Усманов Н.Н.
МГУ
им. М. В. Ломоносова, физический факультет
Исследования нелинейных процессов и эффектов в магнитных или спиновых упорядоченных средах актуальное направление современной электродинамики гиротропных или киральных сплошных сред [1]. Актуальность изучения магнитного упорядочения обусловлена также широким применением магнитных материалов в различных приборах, устройствах радиоэлектроники и компьютерной техники, где магнитная память является основным средством хранения информации.
В работах [2-5] были получены смешанные доменные структуры, состоящие из полосовой доменной структуры и магнитной неоднородности в форме цилиндра и эллипса. В данной работе были получены теоретические зависимости величины максимального изгиба границы полосового домена от параметров ассиметрично расположенной магнитной неоднородности.
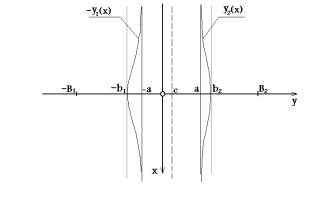
Рис. 1
Рассмотрим
единичный изолированный полосовой домен при наличии внутри него цилиндрической
магнитной неоднородности радиуса R. На рис. 1.
изображен изолированный полосовой домен ширины w=2a,
расположенный вдоль координатной оси x в бесконечной пленке
толщины h, с – параметр несимметричности. Координатная ось z направлена
перпендикулярно плоскости пленки, а ось y – перпендикулярно
доменной стенке. Начало системы координат помещено в центр ЦМД.
Магнитостатическое поле рассеяния данной цилиндрической магнитной
неоднородности исказит форму полосового домена и приведет к зависимости его
ширины от координаты x.
Пусть функции ![]() и
и ![]() определяют изгибы доменных стенок.
Вычисляя вариационные производные функционала изменения магнитостатической
энергии
определяют изгибы доменных стенок.
Вычисляя вариационные производные функционала изменения магнитостатической
энергии ![]() ,
, ![]() , получаем систему нелинейных функциональных интегральных уравнений для
функций
, получаем систему нелинейных функциональных интегральных уравнений для
функций ![]() и
и ![]() , которые при относительно малых искривлениях доменных границ можно
линеаризовать. Раскладывая функции
, которые при относительно малых искривлениях доменных границ можно
линеаризовать. Раскладывая функции ![]() и
и ![]() в пределах интегрирования в ряд,
имеем систему уравнений. Уравнения системы являются линейными интегральными
уравнениями типа свертки и могут быть решены методом преобразования Фурье.
Проводя преобразование Фурье, получим следующие выражения для форм искажения
доменных границ полосового домена:
в пределах интегрирования в ряд,
имеем систему уравнений. Уравнения системы являются линейными интегральными
уравнениями типа свертки и могут быть решены методом преобразования Фурье.
Проводя преобразование Фурье, получим следующие выражения для форм искажения
доменных границ полосового домена:
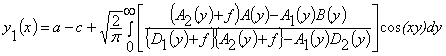 ,
,
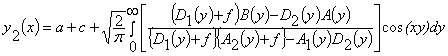 , (1)
, (1)
где
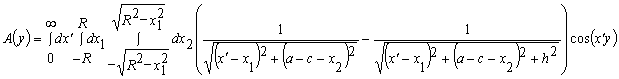
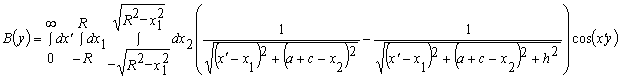
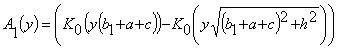 ,
,
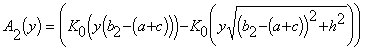 ,
,
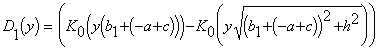 ,
,
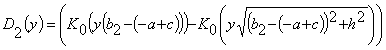 ,
,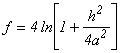 ,
,
![]() и
и ![]() - максимальные
значения функций
- максимальные
значения функций ![]() и
и ![]() , описывающих формы искажений доменных границ
полосового домена вследствие магнитостатического поля рассеяния несимметричного
цилиндрического домена.
, описывающих формы искажений доменных границ
полосового домена вследствие магнитостатического поля рассеяния несимметричного
цилиндрического домена.
С помощью
формул (1) определена форма полосового домена при наличии внутри него
магнитного домена в форме цилиндра.
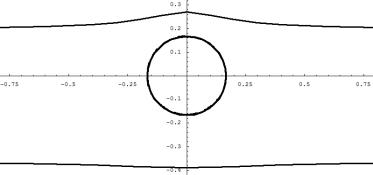
Рис.2
Литературы
[1] L. D. Landau and E. M. Lifshitz. Electrodynamics of continuous
media. Pergamon, Oxford, 1984.
[2] M. L. Akimov and P. A. Polyakov. Vestnik MGU. Ser. 3. Fizika.
Astronomiya. (Bulletin of the Moscow University. Ser. 3. Physics, Astronomy),
2004, № 2, p. 47-50 (in Russian).
[3] M. L. Akimov, Yu. V. Boltasova and P. A. Polyakov. Radiotekhnika
i Elektronika, 46 (2001), p. 504 (in Russian) [Translation: J. Comm. Tech.
Electronics, 46 (2001) p. 469].
[4] M. L. Akimov, P. A. Polyakov and N. N. Usmanov. ZhETF, 121
(2002), 347 (in Russian) [Translation: J. Exp. Theor. Phys., 94(2) (2002),
p. 293].
[5] M. L. Akimov, P. A. Polyakov, Y. V.
Starokurov, N. N. Usmanov, Y. N. Fedyunin. Physica B 405 (2010) 2376.