УДК 622.831
И.У.МАХАМБАЕВА
ОПРЕДЕЛЕНИЕ
ЗОНЫ ВЗАИМОДЕЙСТВИЯ КАРЬЕРА С ПОДЗЕМНЫМИ КАМЕРАМИ В УСЛОВИЯХ ПЛОСКОЙ ДЕФОРМАЦИИ
Прогресс в
экспериментальных методах изучения свойств горных пород позволил выявить новые
важные особенности деформирования пород за пределом прочности,
характеризующиеся разрыхлением и разупрочнением. Тем самым были созданы
предпосылки для разработки новых моделей сред [1,2,3].
На рис. 1
представлен комплекс графиков, характеризующих свойства построенных нами
моделей упругопластической разрыхляющейся среды и среды с разупрочнением с
традиционным условием прочности, обобщенным на область растяжения:
(1)
s1 - s3d = S;
d = ctgy; S = 2*с*ctg (p/4 - j/2),
где ctgy = (1 + sinj)/(1 - sinj); j - угол внутреннего трения; с – сцепление; S –прочность
на одноосное сжатие.
Запредельные диаграммы si - ei (рис. 1) моделей аппроксимируются кусочно-линейными
функциями. Верхние графики зависимостей отражают изменения сопротивляемости
среды по мере деформирования при различных боковых давлениях, нижние–закон
пластического течения. При этом для упругопластической среды (штрих пунктирные
линии на рис. 1с) условие (1) сохраняется для всего процесса деформирования, а
для разупрочняющейся среды сопротивляемость снижается от исходной величины до
остаточной по линейному закону (рис. 1а):
(2) ![]()
S + s3d, если линия (АВН),
Sост + s3dост,
если линия (OMD),
где Sост, dост –
характеристики остаточной прочности.
Пластическое
течение характеризуется параметром l = ctga (рис. 1в).
При l = 1 в условиях плоской деформации объем элемента
среды в ходе пластического течения будет постоянным, при значении l > 1 течение будет характеризоваться
разрыхлением. В частном случае, когда a = y (l = ctgy), разработанная модель соответствует
ассоциированному закону течения.
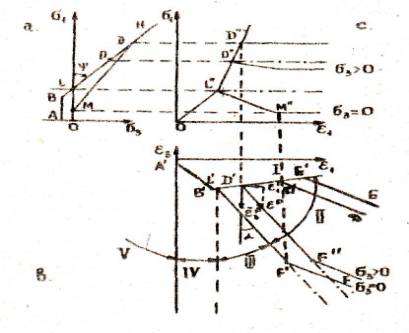
Рис.1. Комплекс графиков характеризующих модели сред
В результате
проведенных исследований в моделях установлены 5 характерных зон: зона
упругости I; зона пластического течения II; зоны одноосного и двухосного разрушения III-V. Причем, для
модели разупрочняющейся и разрыхляющейся среды в зоне II на участках снижения прочности происходит
разрыхление, а в области остаточной прочности необратимая составляющая
изменения объема остается постоянной. В целом значения напряжений в выделенных
зонах определяются использованием семейств линеаризованных графиков
зависимостей
(3)
s3 = f (e1, e3),
s1 = g (e1, e3)
Рассмотрим в условиях плоской деформации на основе разработанной
методики серию решений по определению зоны взаимодействия карьера с подземными
камерами. Проанализированы по отдельности различные варианты. Для всех
вариантов принята одна и та же расчетная конечно-элементная схема. Общие
расчетные параметры таковы: максимальная глубина карьера Н=160 м, угол правого
борта 410, левого - 460,
ширина камеры - 20м, высота -30 м. Все варианты расчитаны на ЭВМ
согласно выбранной
расчетной
схемы поэтапно с постепенной отработкой камер. Сначала
определяются поля напряжений и перемещений для карьера, затем
отрабатывается циклично камеры. В каждом цикле ЭВМ выводит в каждой
точке массива напряжения, деформации, перемещения и информацию о состоянии элемента.
а) Первоначально
задача решается для неподработанного борта карьера. Результаты решения
представлены на рис. 2. Анализ расчетных данных показывает, что зона неупругих
деформаций наблюдается
на подошве откоса в нескольких элементов массива. Направление и величины
главных напряжений
s1
и s3
можно определить по масштабу векторов. Следует отметить, что вектор главных
напряжений вдали от откоса на максимальном расстоянии (ниже подошвы-135м, справа откоса
176 и слева -126) направлено вертикально вверх, потом постепенно выполаживается
и вблизи от поверхности откоса становится параллельным к откосу.
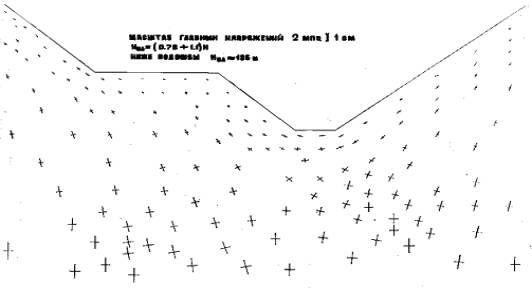
Рис. 2 Неподработанный карьер
Анализ напряженно-деформированного
состояния приконтурной зоне позволяет отметить. что глубина Нвл
проникновения зоны влияния данного карьера достигает Нвл.п.=0.84 Н-
ниже подошвы, Нвл.сп=1.1 Н-справа от откоса Нвлсл.=0.78
Н- слева от откоса. Таким образом
величина влияния карьера изменяется в пределах Нвл..=(0.78+1.1)
Н.
б) После того как
определено напряженно-деформированное состояния всего борта карьера отработаем
1- камеру на глубине 205 м от подошвы левого борта. Результаты расчета показаны
на рис. 3, при этом как показывают векторы главных напряжений
на поверхности камеры они повторяют очертания камеры, а вдали от камеры
становятся вертикальными. Сравнение результатов этого варианта с
результатами неподработанного карьера
дает, что на верхней части камеры главные напряжения s1
и s3 увеличивается соответственно на 3% и 22%. В нижней части камеры
наблюдается уменьшение s1
на 5.5 %, а s3
увеличивается на 22%. В правой части камеры s1 увеличивается на 23%,а s3
уменьшается на 54%. Наконец
вблизи камеры с слевой стороны значение s1
повышается на 30%, s3 -снижается на 68%. Деформации
незначительны. Таким образом, при подработке
напряженно-деформированное состояние массива вблизи камеры
изменяется в широких пределах. Анализ
показывает, что влияние камеры достигает hвл= (0.4+1.4)h м (где h
-высота камеры ). При этом в верхней части hвл.в=0.9h,
нижней
hвл.н=0.8h, с правой стороны - hвл.п=0.4h, с левой
- hвл.сл=0.4h.
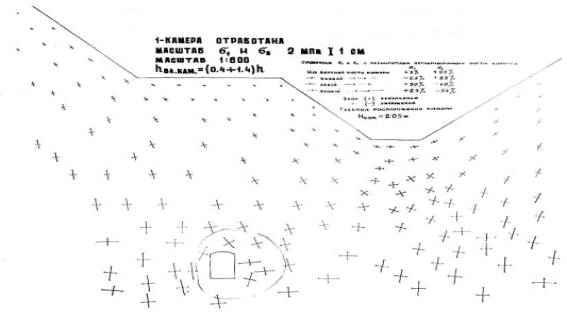
Рис.
3 Подработанный карьер (1- камера
отработана)
в) В этом варианте
отработаем камеру 2, оставляя целик
шириной
18 м от первой камеры. Результаты расчета приведены на рис. 4. Величины напряжения векторов s1
и s3
можно определить по масштабу. Анализ этого
варианта проведем относительно вариантам (а), где имеется одиночная камера.
Зона влияния отработанной второй камерой распространяется вглубь массива на величину hвл=(0.4+1.2)h.
А именно, с левой
и правой стороны камеры hвл.в=0.6h, в верхней части hвл.в=1.2h,
в нижней
hвл.н=0.4h.
Сравнение результатов
расчета по напряжениям показывают, что в правой и левой
части камеры напряжение s1
увеличивается на 26%, а s3
– снижается на 24%. В верхней части имеем снижение s1
на 9% ,повышение s3
на 28 %, в нижней
снижение s1
на 17% и повышение значений
s3
на 16%. Значительные неупругие деформации
не наблюдаются. Для определения устойчивости данного целика, используем критерий разработаный
в [1]. При этом для нашего случая
получим k=2.86, т.е. целик
устойчив.
В целом, численный
анализ выше изложенных вариантов показывают, что зона влияния карьера и подработанных
камер не достигают друг друга, т.е. они
не взаимодействуют.
Борт карьера и целик находятся в устойчивом состоянии.
Список литературы
1.Абдылдаев Э.К.
Напряженно-деформированное состояние массива горных пород вблизи выработок.
Фрунзе., Илим, 1990. – с. 164
2. Фадеев А.Б.
Метод конечных элементов в геомеханике. М.: Недра, 1987 -с. 221
3. Абдылдаев Э.К., Сандибеков М.Н., Заурбекова Н.Д. Моделирование
процесса деформирования откосов. Вестник КазНТУ им. К.Сатпаева №2 (59), 2007.
4. Бызеев В.К.
Обоснование параметров подрабатываемых бортов карьеров при комбинированной
разработке рудных месторождений. Диссертация на соискания ученой степени кандидата технических наук.
Фрунзе,1990,157стр.