Технические науки/1. Металлургия

 

Zhiguts Yu.Yu.1, Gabovda O.V.2, Antalovskyi V.V.1

1Uzhgorod National University, Ukraine

2Mukathevo State University, Ukraine

THE SYNTHESIZED ALLOYS USING THE GEOMETRIC THERMODYNAMIC METHODS

 

The problem of finding the real internal combustion temperatures for exothermic mixtures is that the adiabatic combustion temperatures reach 2400–3500 К, while when being used in combined exothermic reactions with chromium oxide it is 6300 К that exceeds the luminance temperature of the Sun surface. Therefore, the geometric thermodynamic methods are the most expedient to find the alloy phase composition. One has also to take into account that now they are intensively developed and corrected.

The geometric thermodynamic methods developed by the authors allow the alloy phase composition to be clearly found dependent of the chemical composition of the reaction components and of the temperature. The data obtained by the authors are confirmed by the experimental studies on the phase composition [1].

Example of calculation. When using a classical Hillert method [1] and its modifications [2] the most important initial quantity in calculating activities ai along the conoid of the two-phase region of a given isothermal section of the three-component (angle h of the system h-i-j) phase diagram is the activity aiº along the cognominal conoid of the binary system h­i. However, this assumes that the above two-phase region is located close to the diagram h­i. And what about the opposite?

In this case one has to know the activity aiº along at least one conoid of the three-component two-phase region α+β (see fig. 1), and then this conoid will be taken as the basic one though it is inclined towards the axis h­i (νj=0) and the latter is spaced from the region α+β.

Подпись: a+gПодпись: ac<1,0

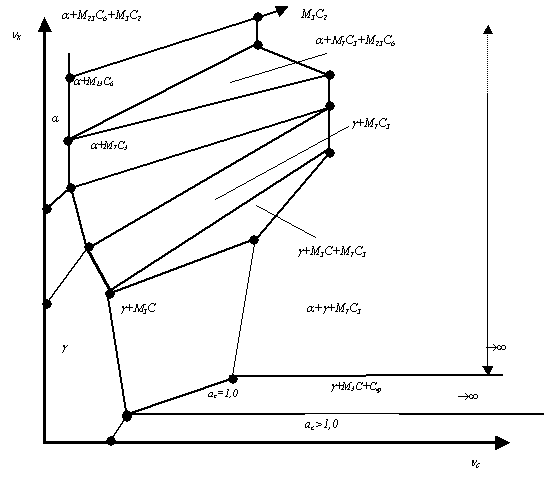
Figure 1. The isothermal section scheme for the phase diagram of the alloys Fe-C-X, in which the graphite at aC>1.0 is produced (provided the graphite is chosen as the carbon standard state) and the carbide phases M3C (cementite), M7C3, M23C6 and M3C2 are produced

 

The isothermal section in fig. 1 is plotted in the Schreinemakers coordinates because this enables a very simple and exact equation to be used in calculations, in which there is no node or figurative alloy point coordinates [1]:

,                                                      (1)

where aiº is the component activity along the basis ("zero") conoid at Xj=0 (the binary system h­і, when the region α+β is adjacent by this conoid to the binary diagram h­i);  is the tangent of the angle of the slope of the two-phase equilibrium conoid in the system under study h­i­j.

All this, in turn, allows one to calculate ai along the conoid in the case shown in fig. 1 using the following equation:

                                 (2)

where ńі and ńо are the tangents of the angles of slope of the conoids αΙβІ and α0β0, respectively; aiδ is a known value ai along the basis conoid α0β0.

Similarly, for the conoid αІІβІІ, the calculation is carried out according to equation:

                       (3)

where  is the αІІβІІ conoid slope.

It is easy to show that the Hillert equation [1] that involves the node coordinates (not saying about the vast approximations required for its derivation) is not fitted for such calculations because at the transition from the conoid α0β0 to the conoid αΙβΙ and then to the conoid αΙΙβΙΙ it is changed essentially.

Figure 1 shows a schematic example of the use of the developed method for the isothermal section (in the supercritical temperature region) in the Fe-C-X-like system (where X is manganese, chromium or their analogues). In the two-phase region g+Cгр austenite+graphite), the carbon activity exceeds 1.0. In the conoid triangle g+M3C+Cгр (austenite+doped cementite+graphite), the carbon activity is by definition aC = 1.0. Above this triangle, aC<1 and these alloys are not capable of graphitizing. The conoid g+M3C of the above triangle is a basic conoid α0β0 (fig. 1) along it aC = 1.0. The use of calculations using equations (2) and (3) in the region g+M3C (just here the activity decreases monotonously down to aC < 1.0) up to the conoid g+M3C of the next conoid triangle g+M3C+M7C3 (the activity aC decreases because ń, and, respectively ń-ń0, increase progressively). In this triangle, the carbon activity is constant and this allows us to use equations (1) and (2) in the calculations for the triangle g+M7C3, where activity aC keeps decreasing with increasing alloy doping degree. The triangle α+γ+M7C3, in the inner part of which the carbon activity is constant, allows one to transfer the value aC from the right bottom conoid of triangle to the upper conoid and to continue calculations using equations (2) and (3) in the triangle α+M7C3. Continuing the above construction for the regions lying above the triangle α+M23C6+M7C3, the tetragon α+M23C6 and the triangle α+M23C6+M3C2, one may extend these calculations to the highly-chrome alloys, though with very high degree of approximation, because the Hillert method is, in principle, elaborated perfectly for the dissolved systems only.

Analysis of the theoretical results. Thus, the successful application of the approximations introduced into the Hillert equation has a certain theoretical basis. The use of the Schreinemakers coordinates instead of the conditional ones provides a unique possibility to simplify and solve the Hillert equation and reduces the number of approximations to the two only, both of them being completely confirmed in the most cases of practical application. The relationships successfully found may give a basis for the certain types of calculations of the ternary phase diagrams provided the principal double diagram and some thermodynamic data related to the alloy element distribution over the phases are known. The results of these calculations are used in the high-temperature studies of alloys and in the cast alloy synthesis by using the combined processes.

The original Hillert method is not suitable to solve a series of tasks related to the high-temperature alloy synthesis, unlike the modified method, that uses the orthogonal Schreinemakers coordinate frame. The reason is that the modified method does not require determination and use of the relevant node coordinates in calculations.

Література:

1. Жигуц, Ю. Ю. Технології отримання та особливості сплавів синтезованих комбінованими процесами [Текст] / Ю. Ю. Жигуц, В.Ф. Лазар. Ужгород: Видавництво «Інвазор», 2014. – 388 с.

2. Жигуц, Ю. Ю. Методика розрахунку складу екзотермічних шихт на основі термохімічного аналізу [Текст] / Ю. Жигуц, В. Широков // Машинознавство. – 2005. – № 4. – С. 48-50.