Современные информационные технологи / 3. Программное обеспечение

к.т.н. Супруненко О.А., магистрант Корольчук А.О.

Черкасский национальный университет имени Богдана Хмельницкого, Украина

ОСОБЕННОСТИ РЕАЛИЗАЦИИ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ СОСТАВЛЕНИЯ РАСПИСАНИЯ ВУЗа

Задача составления расписания ВУЗа заключается в упорядочении некоторого списка работ по времени, месту (аудиторный фонд), исполнителям (преподаватели) и участникам (студенты) работ [1]. В ходе составления расписания также приходится учитывать неоднородность работ (лекции, практические и лабораторные занятия), что вызывает необходимость расстановки приоритетов, в частности по времени их проведения. Например, лабораторное занятие не должно ставиться в расписание после того, как будет прочитана лекция, содержащая соответствующий учебный материал.

Сложность задачи также добавляет то обстоятельство, что исполнители и участники работ могут быть заняты в других работах на некоторые отрезки времени. Наименее часто это встречается в начале заполнения шаблона расписания, по мере решения задачи частота таких ограничений нарастает. Также есть и другие ограничения, например, необходимость проводить лабораторное занятие в соответствующей лаборатории.

Большинство задач теории расписаний есть NP-сложными задачами, потому требуют неприемлемо большого времени решения в случае большой размерности. Задача составления расписания ВУЗа относится к задачам упорядочивания по типу решения [1] и многокритериальным задачам сетевого планирования по типу целевой функции, также она характеризуется большой размерностью. При решении данной задачи в работе применён, приближенный – метаэвристический метод [2] с формированием оценок свободы размещения каждого занятия в шаблоне расписания. Фактически основная задача разбивается на подзадачи и решается путём полного перебора вариантов размещения занятия в расписании, причём таких вариантов тем меньше, чем больше ограничений по входным данным [2]. Таким образом, получаем допустимый вариант расписания ВУЗа.

Оценка качества размещения занятия в расписании считается по формуле:

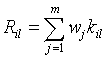
где R_il – оценка качества размещения i-го занятия на l-й позиции шаблона; k_jl – значение оценки размещения занятия в расписании на l-й позиции, полученное по j-му критерию; w_j – весовой коэффициент j-го критерия оценки качества; m – количество критериев оценки качества.

Также сформированы логические функции, которые контролируют ограничения задачи. Например, функция исчезновение “окна” в расписании группы (когда занятие ставится между 1-й и 3-й размещёнными в расписании парами, вследствие чего в расписании возникает последовательность из 3-х пар подряд) равняется 1, если после добавления занятия в данную позицию, в расписании группы исчезает “окно”; 0 – в противоположном случае:

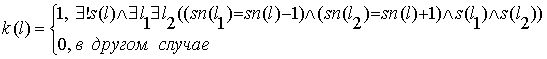
где – булева функция, истинная в том случае, если в l-й позиции расписания у преподавателя есть занятие; – условие существования единственного занятия; – условие существования двух занятий в распи-сании; – функция, которая возвращает номер пари l позиции расписа-ния; – функция, которая возвращает номер пари 3 позиции расписания.

При формировании входных данных для составления расписания составляются списки занятий, которые ранжируются по приоритетности расстановки. В связи с этим велика вероятность, что найденное решение задачи не будет оптимальным. Поскольку критерии ранжирования занятий также являются ограничениями задачи, при их учёте получим допустимый [1] вариант решения за достаточно ограниченное время, что является приемлемым.

Вариант реализации задачи составления расписания ВУЗа можно разделить на два этапа: 1) на основе рабочих учебных планов групп (на семестр) формируется список занятий для размещения в расписании, для каждого занятия рассчитывается оценка свободы размещения занятия, 2) каждое занятие обрабатывается в порядке увеличения рассчитанной оценки, также для каждого занятия рассчитываются дополнительные оценки качества размещения занятия в расписании, из которых выбирается наибольшая.

При использовании данного алгоритма для составления расписания на весь семестр используется модификация, которая учитывает повторяемость занятий на соседних неделях [1]. В начале работы исключаем из списка допустимых для размещения занятий дат праздничные и выходные дни. Рассчитываем количество рабочих дней в семестре по дням недели. Далее составляем расписание для первой недели с учётом ограничений задачи. При составлении расписания на последующие недели для каждой группы, учитываем и стараемся не перемещать занятия, которые были на предыдущей неделе и ещё не вычитались полностью (учитывается модульный принцип вычитки занятий).

В результате функционирования предложенного решения большинство занятий размещаются в расписании, но остаётся часть занятий (при жёстких ограничениях – до 10%), которая не расставлена реализованным алгоритмом. Эти занятия размещаются под основным шаблоном расписания в колонках соответствующих студенческих групп. Дальнейший поиск мест размещения этих занятий в расписании проводиться в диалоговом режиме с пользователем, получающим доступ к редактированию составленного варианта расписания.

Литература:

1. Лазарев А.А., Гафаров Е.Р. Теория расписаний. Задачи и алгоритмы. – МГУ им. Ломоносова. [Электронный документ]. Режим доступа: http://physcontrol. phys.msu.ru/materials/PosobieLazarev/TeorRasp.pdf. Просмотрено 29.11.14.

2. Graham R.L., Lawler E.L., Lenstra J.K., Rinnooy Kan A.H.G. Optimization and approximation in determenistic sequencing and scheduling: a servey // Ann. Descrete Optimization. 1979. V. 2. P. 287-325.