Сатыбалдиев О.С., д.п.н., профессор
Оралов Жандос,
магистрант
Казахский Национальный технический университет имени К.И.Сатпаева
Применение преобразования
Лапласа для решения волнового уравнения
Преобразование
Лапласа играет важную роль при изучении и анализа инженерных систем. Преобразование Лапласа относится к классу интегральных преобразований и
применяется для анализа линейных систем и сигналов. В этой статье
рассматривается применение преобразования Лапласа для нахождения решения волнового уравнения.
Определение 1. Оригиналом
называется функция действительного переменного ![]() определенная при
определенная при ![]() имеющая в каждом
ограниченном промежутке не более конечного числа точек разрыва первого рода и
удовлетворяющая при
имеющая в каждом
ограниченном промежутке не более конечного числа точек разрыва первого рода и
удовлетворяющая при ![]() неравенству
неравенству
![]()
для некоторых чисел ![]() и
и ![]() .
.
Определение 2. Изображением по
Лапласу (преобразованием Лапласа) оригинала ![]() называется функция
вида
называется функция
вида
![]() или
или ![]()
Преобразование
Лапласа ![]() является функцией
комплексного переменного
является функцией
комплексного переменного ![]() .
.
Отметим следующее
свойство оригинала.
Пусть ![]() - дифференцируемый
оригинал,
- дифференцируемый
оригинал, ![]() его изображение,
его изображение, ![]() - оригинал, тогда
- оригинал, тогда
![]()
Следствие. Пусть функция ![]() и ее производные
и ее производные ![]() ,
, ![]() , ...,
, ..., ![]() являются оригиналами,
являются оригиналами,
![]() тогда
тогда
![]()
Рассмотрим волновое уравнение
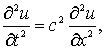
![]()
![]() (1)
(1)
Ищем решение этого уравнения со следующими
начальными и граничными условиями
![]()
![]() (2)
(2)
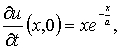
![]() (3)
(3)
![]()
![]() (4)
(4)
![]() при
при ![]() для
для ![]() (5)
(5)
где
![]() - отключение струны
от положения равновесия (искомая функция); из (2) следует, что в начальный
момент времени струна находится в положении равновесия; из (3) следует, что в
начальный момент времени струна имеет начальную скорость колебаний (
- отключение струны
от положения равновесия (искомая функция); из (2) следует, что в начальный
момент времени струна находится в положении равновесия; из (3) следует, что в
начальный момент времени струна имеет начальную скорость колебаний (![]() ); из (4) следует, что левый конец струны закреплен; из (5)
следует, что при удалении
); из (4) следует, что левый конец струны закреплен; из (5)
следует, что при удалении ![]() в бесконечность
отклонение
в бесконечность
отклонение ![]() стремится к нулю.
стремится к нулю.
Для построения решения задачи (1)-(5) используем
преобразования Лапласа. К обеим частям уравнения (1) применяем преобразование
Лапласа
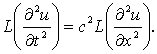 (6)
(6)
Известно, что
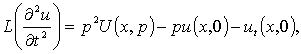 (7)
(7)
где
![]() .
.
Так как ![]()
![]() (см. (2)-(3)), то
равенство (7) перепишем в виде
(см. (2)-(3)), то
равенство (7) перепишем в виде
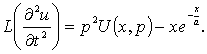 (8)
(8)
Рассмотрим выражение
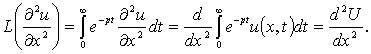 (9)
(9)
С учетом (8)-(9)
равенство (6) перепишем в виде
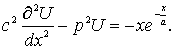 (10)
(10)
Характеристическое
уравнение соответствующего однородного уравнения имеет вид
![]()
При этом общее
решение соответствующего однородного уравнения имеет вид
![]()
где ![]() и
и ![]() - произвольные
постоянные.
- произвольные
постоянные.
Частное решение неоднородного
уравнения (10) будем искать в виде
![]()
Тогда общее решение
уравнения (10) есть сумма ![]() .
.
Если к обеим частям
(4) и (5) применим преобразование Лапласа, то получим следующие граничные
условия относительно ![]()
![]()
![]() при
при ![]()
Эти условия будем
использовать для нахождения значений произвольных постоянных ![]() и
и ![]() .
.
Использование
формулы ![]() и соотношения
и соотношения
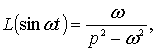
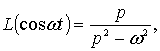
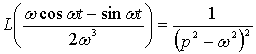
дает решение задачи (1)-(5) в виде
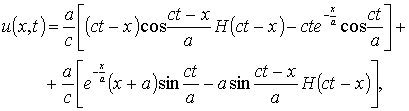
где ![]() - функция Хевисайда,
- функция Хевисайда, ![]() обратное преобразование
Лапласа.
обратное преобразование
Лапласа.
Литература
1. Отелбаев М. Оценки спектра
эллиптических операторов и связанные с ними теоремы вложения. Докт. …, дис. – М.: МГУ, 1978.
2. Guzman M. A covering lemma vith application so
differentality of measures and singular integral operators, studio, Math., 34,
№3, 1970, 299-370.
3.
Келдыш М.В. О собственных значениях и собственных функциях некоторых классов
несамосопряженных уравнений, ДАН СССР, 77, №1 (1951), 11-14.