МАТЕМАТИКА/5.Математическое моделирование

к.ф.-м.н. Искакова А. С., Токсанова С.С.

Евразийский национальный книверситет имени Л.Н. Гумилева, Астана, Казахстан

ОБ ОДНОЙ МОДЕЛИ ПРОГНОЗИРОВАНИЯ CОЦИАЛЬНЫХ ВЫПЛАТ СТРАХОВОГО ПОРТФЕЛЯ ПО БЕРЕМЕННОСТИ И РОДАМ

Модели прогнозирования, как отражение существующей реальности, оказываются совершенно необходимыми для описания очень многих явлений и ситуаций, встречающихся в повседневной жизни.

Одной из характерных особенностей поставленных перед управлением страховыми компаниями Республики Казахстан является составление прогнозов социальных выплат страхового портфеля.

Рассмотрим построение эмпирической функции«страховой компании» выплата по беременности и родам, заданной графически.

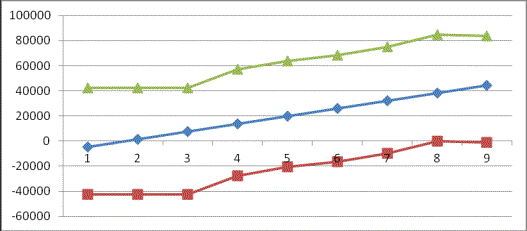
По консолидированной финансовой отчетности АО «Государственный фонд социального страхования» имеем статистические данные за последние 9 лет.

Нас интересует, как выглядит функциональная зависимость между x_i и y_i, где i принимает любые натуральные конечные значения.

Пусть y – функция одной переменной с двумя параметрами a и b. В качестве набора выбора функций, из которых будем иметь эмпирическую зависимость, рассмотрим:

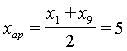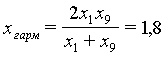Для наилучшего выбора вида аналитической зависимости y=f(x,a,b) построим следующие промежуточные вычисления. На заданном отрезке изменения независимой переменной выбирают точки, достаточно надежные и, по возможности, далеко отстоящие друг от друга. Будем считать, что это x₁ и x_k. арифметическое, среднее геометрическое и среднее гармоническое . По вычисленным значениям независимой переменной находим из статистических данных соответствующие значения переменной , , для пока еще неизвестной аналитической зависимости y=f(x,a,b).

Теорема. Пусть . Тогда

1. если e=e₁, то в качестве аналитической зависимости для данного графика хорошим приближением служит линейная функция ;

2. если e=e₂, то в качестве аналитической зависимости для данного графика хорошим приближением служит показательная функция;

3. если e=e₃, то в качестве аналитической зависимости для данного графика хорошим приближением служит дробно-рациональная функция ;

4. если e=e₄, то в качестве аналитической зависимости для данного графика хорошим приближением служит логарифмическая функция;

5. если e=e₅, то в качестве аналитической зависимости для данного графика хорошим приближением служит степенная функция:

6. если e=e₆, то в качестве аналитической зависимости для данного графика хорошим приближением служит гиперболическая функция

7. если e=e₇, то в качестве аналитической зависимости для данного графика хорошим приближением служит дробно-рациональная функция .

Доказательство теоремы можно найти в разных учебниках по таким направлениям как «Численные методы», «Математический анализ», «Теория вероятностей и математическая статистика». Проводя сравнение, получаем . Следовательно, в качестве аналитической зависимости следует выбрать гиперболическую функцию . Для уточнения коэффициентов выбранной аналитической зависимости воспользуемся методом наименьших квадратов. Аналогично, вычислениям, проводимым при рассмотрении дохода добровольного личного страхования, находим a= 12357861,05

и b= -24787036492

. Таким образом, подставляя найденные коэффициенты в выражение , получаем аналитическое выражение эмпирической функции прочих выплат

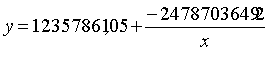
Список литературы

1. Данилина Н.И. и др. Численные методы.

2. Малыхин В.И. Финансовая математика. –М.:Юнити, 2003. -237 с.

3. Волков И., Загоруйко Е. Исследование операций. М-2002.

4. Искакова А.С. Условие существования оценок максимального правдоподобия для параметров одного класса многомерных распределений // Известия МОН РК, НАН РК. 2004 г. №1. – С. 90-95.

5. Ледерман Э., Справочник по прикладной статистике т.2, – М., Финансы и статистика. 1990