Математика/5. Математическое моделирование

Денисюк О.Р.

Украинский государственный химико-технологический университет, Украина

Один возможный способ применения математического моделирования для определения плотностных и магнитных свойств геологических объектов по измеренным гравитационным и магнитным аномалиям (двумерный вариант)

Математическое моделирование широко используется в геофизических методах исследований, которые позволяют по измеренным значениям физических параметров с той или иной точностью определять строение и свойства изучаемых геологических объектов. При этом, в соответствии с принципом модельности, с помощью цепочки гипотез, идеализаций и упрощений определяют физическую модель изучаемого разреза, модель физического поля, представленную измеренными его значениями в дискретных точках профиля, и модель их взаимосвязи, устанавливающей связь между распределением в среде рассматриваемого физического параметра и распределением измеренных значений изучаемого поля. Учитывают также модели помех, осложняющих исходные данные и, в частности, измеренные поля. В данной работе рассмотрения проводятся для магнитного и гравитационного полей. Эти поля являются потенциальными. Их совместная интерпретации базируется на близости физико-математического аппарата. С другой стороны, в ряде случаев, особенно при решении задач рудного типа, эти методы дополняют информацию друг друга и позволяют решать общий круг задач.

При интерпретации магнитных и гравитационных аномалий важно знать кроме измеренных значений магнитных аномалий или и гравитационной аномалии также значения намагниченностей и плотностей горных пород, слагающих геологический разрез. От этого зависит достоверность и эффективность интерпретации аномалий.

Один из методов определения намагниченностей и плотностей горных пород, слагающих изучаемый геологический разрез, состоит в измерении их в лаборатории на образцах горных пород, отобранных из обнажений и скважин. По разным причинам этот подход не всегда возможен, и актуальной становится задача определения указанных свойств по измеренным значениям магнитных и гравитационных полей изучаемых объектов. Определение намагниченности и плотности горных пород по создаваемым ими магнитным и гравитационным аномалиям представляют соответственно обратную линейную задачу магниторазведки и гравиразведки. Решения таких задач в связи с их некорректностью весьма неоднозначны и неустойчивы даже при их линейной постановке. Общие положения теории решения некорректно поставленных линейных обратных задач изложены в работах А.Н Тихонова [1], В.И. Старостенко [2], В.Н. Страхова [3] и др.

В данной работе разработаны алгоритм и программа определения плотности и намагниченности горных пород геологического разреза на основании измерений гравитационных аномалии или магнитных аномалий или соответственно. Проведены испытания на различных моделях и тестах и апробация на полевых материалах в условиях Украинского щита.

Рассмотрим сначала модельные представления, принятые для исследуемых объектов. Все рассмотрения проведены в двумерном варианте, то есть предполагается, что аномалии создаются бесконечными телами сложного сечения, для которых влиянием удаленных вдоль оси простирания масс можно пренебречь. Как известно, такая идеализация правомерна для геологических объектов, длина которых более чем в 5 раз превышает их мощность. В этом случае можно проводить интерпретацию по одному профилю, ориентированному вкрест простирания объекта. Основные выводы работы могут быть распространены и на трехмерные модели.

Выбранная для аппроксимации среды модель, удобна для описания тел рудного типа, но, в принципе, может описывать и слоистые среды. Пусть имеется несколько однородных по плотности и намагниченности двухмерных тел произвольного сечения, простирающихся вдоль одной и той же оси . Обозначим номер тела . Выберем систему прямоугольных координат таким образом, чтобы изучаемый разрез находился в одном квадранте, и направим ось направо, а ось - вниз. Пусть также на профиле, пересекающим тела вкрест простиранию, измерены в ряде точек , с координатами , гравитационная аномалия и/или магнитные аномалии или (свободные от фона или осложненные фоном, близким к линейному). Задача состоит в том, чтобы по измеренному на профиле распределению данных полей и известным формам и размерам сечений двухмерных тел определить величину избыточной плотности каждого тела - или проекции векторов намагниченности элементарных тел модели (число неизвестных в этом случае 2). Вводятся также следующие упрощения: предположение об отсутствии аномальных магнитных и плотностных масс вне области ; рассмотрение намагниченности и плотности как независимого параметра вне связи с другими параметрами, описывающими распределение аномалиеобразующих масс; предположения о том, что все источники магнитного либо гравитационного поля расположены в нижнем полупространстве, что каждый элементарный объект области имеет свою, но постоянную намагниченность и плотность, а намагниченность и плотность вмещающей среды тоже постоянны.

Как известно, в такой общей постановке задача не имеет единственного решения [4, 5 и др.]. Однако можно выделить классы тел, для которых единственность решения плоских обратных задач гравиразведки и магниторазведки в линейной постановке имеют место. Одним из таких классов являются тела с многоугольным сечением [2]. Если же факт единственности установлен, то применение регуляризующих алгоритмов гарантирует приближение к искомому решению, согласованному по точности с точностью входных данных.

Рассмотрим теперь модель связи изучаемых параметров. Гравитационный эффект одного -го тела геологического разреза в -ой точке профиля равен сумме эффектов всех уступов его аппроксимационной конструкции и является функцией координат его угловых точек, координаты точки профиля, где вычисляется поле, и плотности уступа: 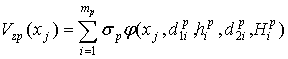, где и - координаты верхней и нижней угловых точек уступа соответственно. Гравитационный эффект всех двумерных тел геологического разреза в -ой точке профиля равен сумме их эффектов, и для определения плотностей всех тел геологического разреза необходимо составить систему уравнений:

,

решая которую относительно , можно определить плотности горных пород всех тел геологического разреза.

Аналогично магнитные аномалии или в -ой точке профиля можно вычислить по следующим уравнениям [6]:

,

- нормальное магнитное наклонение и магнитный азимут профиля;

- вторые производные гравитационного потенциала, обусловленные геологическими объектами разреза, рассчитанные при плотности где - гравитационная постоянная.

Таким образом, задача определения плотностей либо намагниченностей тел геологического разреза сводится к решению переопределенной системы линейных алгебраических уравнений типа

,

где оператор А — это некоторое отображение, задающее связь модели среды и поля (оператор прямой задачи), — вектор параметров (физические свойства - плотность либо намагниченность или геометрические параметры аппроксимационных тел, класс - некоторое множество моделей среды, каждый элемент которого является допустимым для задачи), U — измеренное поле - вертикальная производная либо другая компонента гравитационного потенциала либо компоненты магнитного потенциала, в зависимости от рассматриваемой задачи, (класс - множество моделей поля). При этом сам вид оператора А, как видно, существенно различен в случае задач нахождения плотности или намагниченности. Однако в такой постановке видна общность этих задач. В данной работе ограничимся рассмотрением случая, когда требуется определить свойства ,источников поля, если задано поле и закреплена геометрия источников поля; как отмечалось, эта задача является обратной линейной задачей гравимагниторазведки.

Как отмечалось выше, особенность последнего уравнения состоит в том, что матрица и правая часть системы заданы приближенно: , , где - точное значение поля, - точная матрица, и - погрешности задания значений поля и элементов матрицы.

Фундаментальным приемом решения некорректно поставленных систем уравнений является метод регуляризации А.Н. Тихонова [1], который сводится к минимизации сглаживающего параметрического функционала

,

где - параметр регуляризации, согласованный с погрешностями входных данных и , норма рассматривается в пространстве . Доказано [1], что решение обратной задачи является регуляризующим и позволяет по приближенно заданным входным данным и и их погрешности построить такое решение , что при , где - точное решение задачи. Минимизация рассматриваемого функционала сводится к решению системы уравнений:

,

где - транспонированная матрица , а - единичная матрица. Решение этой системы уравнений позволяет найти искомые параметры (плотности или намагниченности пород) всех тел геологического разреза, создающих соответствующую аномалию на профиле. Трудность в этом алгоритме представляет выбор параметра . Его нельзя вычислить заранее, так как неизвестны ошибки входных данных и . Поэтому минимизацию функционала выполняют на некоторой сетке значений параметра регуляризации , которую строят, например, в виде геометрической прогрессии со знаменателем .

Для выбора оптимального значения и соответственно оптимального решения задачи А.Н. Тихонов и В.Б. Гласко предложили эвристический метод выбора по минимуму функции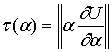 , которую численно можно вычислять по формуле:

.

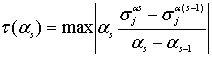На поведение этой функции влияют многие факторы - характер оператора А, уровень ошибок во входных данных и , поэтому данная функция имеет ряд минимумов, что затрудняет выбор квазиоптимального параметра регуляризации. В данной работе разработан и другой критерий. Численными экспериментами установлено, что при положительных значениях параметра регуляризации функция непрерывна и строго монотонно возрастает. Установлено также, что параметр принимает квазиоптимальное значение, , в том случае, когда функция имеет максимальную кривизну, т.е функция достигает максимума. Таким образом, находя экстремали функционала А.Н. Тихонова на сетке значений параметра , , s=0, 1, 2,... и каждый раз вычисляя в конечных разностях по формуле

по ее максимуму можно определить и приближенное решение задачи.

Описанный алгоритм реализован в виде программы на языке C# для программной платформы Microsoft.NET Framework 2.0. Проведены тестовые испытания на модельных примерах. Гравитационные и магнитные поля над моделями были вычислены путем решения соответствующих прямых задач. Они свободны от влияния случайных ошибок и регионального фона. Для исследования влияния ошибок измерения полей к вычисленным точным значениям поля добавлялись случайные ошибки различного уровня, распределенные по нормальному закону. Распределение ошибок моделировалось с помощью датчика случайных чисел. Программа позволяет также выполнять вычисления в случае, если исходные поля осложнены фоном, близким к линейному. Для снятия фона использована простейшая трансформаций поля – вариация Андреева. Тестирование этого режима программы также дало хорошие результаты.

Испытание различных режимов работы программы на тестовых примерах позволило сделать следующие выводы: решение задачи устойчиво, построенный критерий позволяет выбрать квазиоптимальное решение, уровень погрешностей в результатах соответствует уровню ошибок во входных данных, полученные результаты гораздо точнее, чем при решении задач без регуляризации, точности определения плотности либо намагниченности пород соизмеримы с точностью их определения в лаборатории на образцах пород.

Положительные результаты испытаний программы на теоретических моделях дали возможность применить ее для определения избыточной плотности и намагниченности комплексов пород в условиях Верховцевской структуры Украинского щита по измеренным значениям поля , и . Вычисленные значения плотностей и намагниченностей комплексов пород достаточно хорошо совпадают с данными практических определений этих параметров на образцах горных пород. Имеется акт внедрения программы.

Таким образом, в соответствии с основными принципами математического моделирования, создав последовательность «модель-алгоритм-программа» и установив на вычислительных экспериментах ее адекватность и работоспособность, полученный инструмент был опробован для решения конкретных геологических задач и дал позитивные результаты.

Литература

1. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач.

- М.: Наука, 1979. - 235 с.

2. Старостенко В.И. Устойчивые численные методы в задачах гравиметрии. К.: Наукова думка, 1978. - 227 с.

3. Страхов В.Н. Некоторые примеры эквивалентности и слабой единственности в плоской обратной задаче потенциала. Известия АН СССР. Физика Земли, 1973, № 5, с. 39 - 62.

4. Бродский М.А., Страхов В.Н. О единственности решения двухмерных обратных задач гравиметрии и магнитометрии для многогранников. Доклады АН СССР, 1982, т. 264, № 2 , с 318 - 322.

5. Страхов В.Н., Лапина М.И. Прямая и обратная задача гравиметрии и магнитометрии для произвольных однородных многоугольников. В кн. Теория и практика интерпретации гравитационных и магнитных полей в СССР. Киев, Наукова думка, 1983, с. 3-87.

6. Гравиразведка. Справочник геофизика. / Под. ред. Е.А. Мудрецовой, К.Е. Веселова. - М.: Недра, 1990. - 607 с.