Физика./10 Физика полимеров.

Байджанов А.Р., Баруздина О.С., Моисеева А.И.

Череповецкий государственный университет, Россия

Определение макроскопических характеристик симулированной полимерной системы.

Согласно теории разрушения Сяо-Кауша [1] механические свойства твердых тел определяются преимущественно ориентацией его элементов, что подтверждается рядом экспериментов по исследованию прочности и долговечности полимерных материалов [2]. В работе [3] показано, что прочность ориентированного полимера в 10-15 раз выше неориентированного.

При моделировании полимерной системы, модель которой приведена выше, необходимо определить граничные условия. Для минимизации эффекта конечности системы вдоль осей n₂ и n₃ введены периодические граничные условия.

Для определения параметров ориентационного порядка и других макроскопических характеристик в данной работе использовался следующий алгоритм.

1. Формирование начальной конфигурации произвольно ориентированных ротаторов в решетке. Предполагалось, что величина сферического угла имеет равномерное распределение в промежутке [0; 2]. Так как координатные q - линии сферической системы координат имеют различную длину, в данной работе равномерное распределение выбрано не для величины угла , а для значения функции . В ячейках с n₁ = 1 полимерные цепи взаимодействуют с металлом. Поэтому ротаторы в этих ячейках могут быть свободными () или закрепленными () с вероятностью, равной коэффициенту прилипания σ, рассмотренном в предыдущих пунктах. В ячейках с n₁ = N₁ введены свободные граничные условия.

2. На каждом шаге Монте – Карло (n_МК) случайно выбиралась одна из ячеек решетки, определялись энергия находящегося в ней ротатора. Учитывались взаимодействия только с соседними сегментами.

3. Случайным образом изменялась конфигурация ячейки решетки и вычислялась новая энергия конфигурации E, которая может быть, как меньше, так и больше первоначальной E₀. Если происходит понижение энергии системы, то ей приписывается новое конфигурационное состояние. В противном случае производится генерация случайного числа в интервале (0; 1) и производится его сравнение с величиной больцмановского фактора, вычисляемого по формул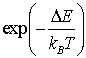е . Если она оказывается больше сгенерированного числа, то система переходит в состояние с более высокой энергией. Если же этого не происходит, то ансамблю ротаторов приписывается исходное конфигурационное состояние.

4. Таким образом, при достаточно большом значении числа шагов Монте-Карло система приходит в состояние, соответствующее заданному значению температуры и энергетических и геометрических параметров модели в соответствии с химическим строением и модификацией полимерного покрытия. Полученная конфигурация позволяет определить средние практически всех термодинамических величин (параметр порядка, теплоемкость, восприимчивость и др.).

На рис. 1 приведены вычисленные с помощью алгоритма Метрополиса зависимости дальнего ориентационного порядка. В качестве параметра порядка в системах с дипольными взаимодействиями принимается средний косинус угла между направлениями ротатора и директора.

Показано, что упорядоченная система меняется при изменении температуры скачком и на рис. 1 приведены фазовые диаграммы, также на рисунке приведены рассмотренные конфигурации полимерной системы при низкой и высокой температуре.

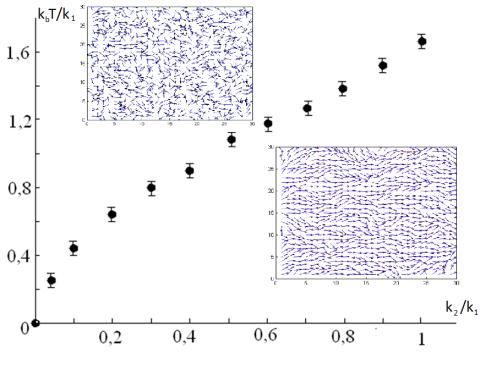
Рисунок 1. Фазовая диаграмма. Зависимость между энергетическими параметрами модели в критической точке (Фазовая диаграмма), вычисленная с помощью метода Монте Карло.

Литература:

1. О. Г. Максимова, А. В. Максимов, Е. В. Ершов,Т. О. Петрова, И. А. Варфоломеев. Модели, методы и алгоритмы оптимального управления формированием поверхностных слоев и пленочных полимерных покрытий металлического листа. ЧГУ, 2013. 256 с.

2. C. C. Hsiao1, S. R. Moghe1 and H. H. Kausch von Schmeling1, J. Appl. Phys.,39, pp.4915-4919 (1968)

3. Г.Кауш. Разрушение полимеров. М. Мир. 1981. 440 с.