Строительство и архитектура/3. Современные технологии строительства реконструкции и реставрации

Профессор Бубнович Э.В., магистрант Бондаренко Д.М.

Казахстанский национальный технический университет им.К.И.Сатпаева

К вопросу об уравнениях колебаний радиальных вантовых систем

Рассматривается пологая двухпоясная радиальная вантовая система кругового очертания в плане. Различные виды таких систем (рис.1-3) не отличаются друг от друга как с точки зрения статического, так и динамического расчета. Континуальная модель каждого из поясов радиальных вантовых систем представляет собой однопараметрическое семейство нитей, закрепленных в наружном опорном контуре и внутреннем кольце. Связи между напрягающими и несущими вантами считаются недеформируемыми и непрерывно распределенными. Внутренние кольца имеют конечные размеры, однако их изгибной жесткостью и горизонтальными силами инерции будем пренебрегать.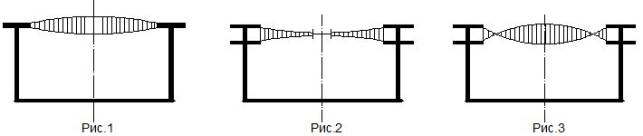

Нити обоих поясов, при отсутствии тангенциальных компонент внешней нагрузки, направлены вдоль геодезических линий кривизны соответствующей поверхности, а усилия в каждой из них постоянны. Таким образом, нити радиальной системы образуют семейство геодезических линий кривизны, чем и объясняется их высокая экономичность: при прочих равных условиях теоретический вес радиальной системы в полтора раза меньше, чем ортогональной сетки.[2]

Дается вывод обыкновенных дифференциальных уравнений колебаний радиальной вантовой системы, рассматриваемой как система с двумя степенями свободы.

В качестве системы координат принимаются полярные координаты () с полюсом, совпадающим с проекцией на эту плоскость узлов верхнего и нижнего поясов.

Основное дифференциальное уравнение колебаний двухпоясной радиальной вантовой системы при отсутствии тангенциальных компонент внешней нагрузки имеет вид: [1]

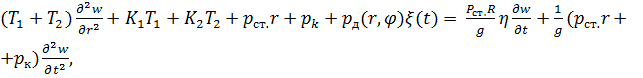(1)

где

; (2)

;

и - усилия в несущих и напрягающих вантах соответственно, относящиеся к полоске полярного угла = 1, т.е. к сектору, содержащему определенное постоянное число нитей;

и - усилия предварительного напряжения;

и - кривизны начальных линий равновесия вант;

и - жесткость нитей на растяжение;

и - радиальные перемещения несущих и напрягающих вант;

w – прогиб сетки; – равномерно распределенная статическая нагрузка; - вес внутренних колец (барабана) на единичный полярный угол; - осесимметричная динамическая нагрузка; – коэффициент демпфирования; – ускорение силы тяжести.

Благодаря отсутствию связи между вантами в кольцевом направлении структура уравнений (1) и (2) такова, что угловая координата играет роль параметра.

Аппроксимирующую функцию прогиба сетки примем в виде [2]

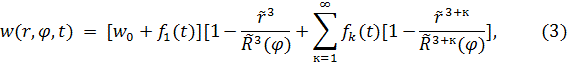
где , (k = 1,2,3,…) – статическое и динамическое поперечные перемещения сетки;

– радиус наружного опорного кольца; - радиус внутреннего кольца.

Система координатных функций в (3) удовлетворяет условиям:

1) все элементы принадлежат гильбертову пространству Н;

2) при любом k ее элементы линейно независимы;

3) последовательность функций полна в Н.

Подвергая (3) ортогонализации с весом и ограничиваясь первыми двумя членами ряда, будем иметь

Здесь = = const.

Из уравнений (2) найдем

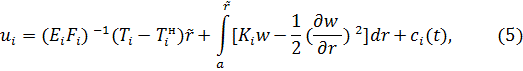
где - произвольные функции времени, определяемые из нулевых граничных условий на внутреннем контуре;

= – начальные стрелки провеса несущих и напрягаемых вант, (i = 1,2).

Принимая во внимание нулевые граничные условия на опорном контуре и внося (4) в (5), приведем последние к виду

где

Подставляя (4) и (6) в уравнение (1) и применяя метод Бубнова-Галеркина, приходим к системе двух нелинейных дифференциальных уравнений, которые в матричном виде запишутся следующим образом:

(7)

Здесь

представляют собой симметричные матрицы масс, вязкого демпфирования и жесткости;

{}; {} – векторы обобщенных координат и интенсивности динамической нагрузки; – вектор нелинейного влияния равный:

,

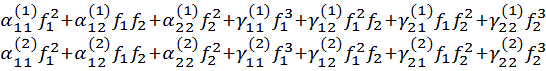– динамическая нагрузка.

Коэффициенты в матрицах и векторах V и имеют вид

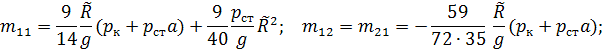
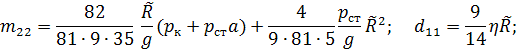
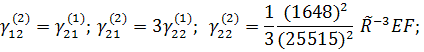
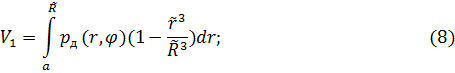
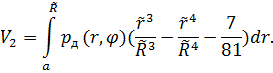
Величина статического прогиба определяется из кубического уравнения:

в котором

(9a)

;

Из матричного уравнения (7) видно, что радиальная вантовая система является полной системой, состоящей из нескольких (двух) парциальных систем. Каждая парциальная система, соответствующая своей обобщенной координате, обладает определенной собственной частотой, как система с одной степенью свободы:

(10)

Члены с и характеризуют связь между этими системами. При этом коэффициент инерционной связи определяется как:

а коэффициент упругой связи равен

.

Из анализа влияния связи на собственные частоты вантовой системы видно преобладание упругой связи, увеличение которой будет приводить к удалению друг от друга собственных частот системы, а уменьшение – к их сближению.

Литература:

1. Ивович В.А., Динамический расчет висячих конструкций. М., Стройиздат, 1975.

2. Бубнович Э.В., Калдыгазов К.Б., Колебания вантовой сетки при воздействиях типа сейсмических. Вестник КазНТУ им. К. Сатпаева. Алматы, 2014, №4.